La legge

L'ellisse percorsa da un pianeta attorno al Sole ha una forma simmetrica, ma il moto non è simmetrico.

    Pensate a un sasso gettato verso l'alto. Mentre sale perde velocità... quindi per un istante, al culmine della traiettoria, si muove appena impercettibilmente... e infine ricade giù, guadagnando di nuovo velocità. In un certo qual modo, anche un pianeta intorno al Sole, oppure un satellite artificiale intorno alla Terra, si muovono allo stesso modo, benché le equazioni del moto siano differenti.

    Questo è soprattutto evidente se l'orbita è allungata, cioè se l'eccentricità è grande. Quando il pianeta o il satellite "sale" nella sua orbita (cioè si allontana dal corpo attorno a cui ruota), esso rallenta, e poi, quando ritorna, riprende di nuovo velocità. Si muove quindi più velocemente quando si trova nel punto più vicino, nel punto dell'orbita chiamato perielio per un pianeta ("Helios" in greco è il Sole) e perigeo per un satellite della Terra ("geo" indica, sempre dal greco, qualcosa collegata con la Terra).

    Dopo aver studiato i dati osservativi, soprattutto riguardanti Marte, Keplero propose la seguente regola per prevedere l'aumento e la diminuzione della velocità. Tracciamo una linea ("raggio vettore") dal centro del Sole al pianeta (o dal centro della Terra al satellite). La legge di Keplero afferma:

"Il raggio vettore spazza aree uguali in tempi uguali"

Uno schema che illustra la seconda  legge di Keplero: i tratti di orbita AB  e CD sono percorsi in tempi uguali.

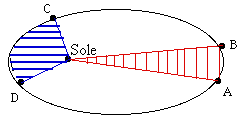
    Come esempio, supponiamo che il disegno qui a destra rappresenti l'orbita di un pianeta che ruota intorno al Sole, e siano AB e CD due tratti di orbita percorsi in 3 ore vicino all'afelio e vicino al perielio, rispettivamente. Se quindi O è il centro del Sole, le aree tratteggiate OAB e OCD sono uguali. Questo significa ovviamente che CD è molto più lungo di AB, poiché vicino al perielio il pianeta si muove molto più rapidamente e percorre una distanza molto maggiore nelle stesse 3 ore.

            Energia

    L'energia può essere grossolanamente definita come un qualcosa che faccia muovere una macchina. Le forme di energia che alimentano le nostre macchine in genere sono l'elettricità o il calore. Anche la luce è un'altra forma di energia, convertita in elettricità dalle celle solari che alimentano la maggior parte dei satelliti artificiali.

    Anche la gravità fornisce energia. Le lancette degli orologi a pendolo dei nostri nonni erano fatte muovere da un peso che gradualmente scendeva fino al fondo dell'orologio, e a quel punto bisognava riportarlo in alto, altrimenti l'orologio si fermava. Thomas Jefferson, nella sua casa a Charlottesville, in Virginia, aveva un orologio i cui pesi (attaccati su un lato della stanza) erano costituiti da palle di cannone legate a una corda, e, per dare all'orologio un'autonomia di 7 giorni, era stato praticato un foro nel pavimento per consentire alle palle di cannone di scendere fino nello scantinato.

    Quando un peso (o una palla di cannone) viene sollevato vincendo la forza di gravità, esso acquista un'energia potenziale -- un'energia dovuta alla sua posizione, proporzionale all'altezza a cui è stato sollevato. Se il peso viene fatto cadere, esso perde la sua energia potenziale, ma guadagna velocità e quindi energia cinetica, l'energia cioè dovuta alla velocità del suo moto. L'energia cinetica può essere convertita di nuovo in energia potenziale, come avviene per un vagoncino dell'otto volante quando passa nel punto più basso di una discesa e ricomincia a salire di nuovo.

    Un simile cambiamento avviene quando si getta un sasso verso l'alto con una certa velocità v. Se la sua massa è m (la massa sarà definita più avanti, ma per ora possiamo considerarla come qualcosa associata al peso), si può dimostrare che la sua energia cinetica è

1/2 mv²

Quando il sasso sale, v e la sua energia cinetica diminuiscono, ma questo è compensato dal contemporaneo aumento di energia potenziale

h m g

dove h è l'altezza in metri e g è una costante che misura l'intensità della forza di gravità: se m è espressa in chilogrammi, h in metri e v in metri al secondo (scritto m/sec; la velocità di una persona che cammina è di circa 1-2 m/sec), g vale circa 9,81.

La somma delle due forme di energia è l'energia totale E e rimane costante:

E  =   1/2 mv² +  h m g = costante

    Quando il sasso sale verso l'alto, la parte cinetica della sua energia diventa sempre più piccola, diventando zero quando il sasso raggiunge il punto più alto, in cui per un breve istante v = 0. Nel tratto in cui ridiscende, avviene l'opposto. In una prossima sezione torneremo sulla formula precedente e al concetto di energia.

Per un satellite di massa m in orbita attorno alla Terra (o per un pianeta in orbita attorno al Sole) esiste una formula simile:

E = 1/2 mv² – k m/r = costante

    Qui k è un'altra costante -- collegata a g, poiché entrambe le costanti sono connesse con l'intensità della gravità terrestre (il valore esatto è is k = g R², dove R è il raggio della Terra, in metri). Non fatevi confondere dal segno meno: mentre il satellite va più in alto, r aumenta, km/r diventa più piccola, ma –km/r diventa più grande, poiché è meno negativa rispetto a quando il satellite era più vicino alla Terra. Questa equazione mostra perché la velocità del satellite diminuisce quando si allontana dalla Terra e aumenta quando si avvicina di nuovo.

            L'anomalia media

    Si è affermato precedentemente che è necessario un terzo elemento orbitale per specificare dove è posizionato il satellite lungo l'orbita. Poiché l'equazione dell'ellisse orbitale è

r = a(1 – e²)/(1 + e cos f)

ciascun valore dell'angolo f -- chiamato "anomalia vera" -- specifica una posizione lungo l'orbita. Si può quindi usare l'anomalia vera come terzo elemento orbitale.

    L'anomalia vera  f  varia periodicamente lungo l'orbita, rapidamente vicino al perigeo e lentamente vicino all'apogeo. La seconda legge di Keplero fornisce tutti i dettagli di questa variazione e dovrebbe consentirci di ottenere una formula che esprima il modo con cui  f  varia in funzione del tempo t. Purtroppo non esiste un modo semplice per esprimere tale formula.

    Il modo più semplice per esprimere  f  è quello di usare due angoli ausiliari, che, come  f , aumentano di 360 gradi ogni orbita, "l'anomalia eccentrica" E (la lettera E non ha qui niente a che vedere con l'energia) e "l'anomalia media" M. Esiste allora un'equazione che correla  f  con E, e un'altra che correla E con M. Il gran vantaggio di  M è che essa aumenta proporzionalmente al tempo t:

M = M(0) + nt

dove M(0) è il valore di M quando t = 0 e n è una costante (correlata alla costante che compare nella terza legge di Keplero). L'anomalia media è quella che viene usata come terzo elemento orbitale.

Se si vuole prevedere la posizione di un satellite sulla sua orbita a un dato istante di tempo t, assumendo che il moto ellittico delle leggi di Keplero sia approssimato abbastanza bene per una tale previsione (trascurando l'attrazione lunare, l'attrito dell'alta atmosfera, ecc.), il primo passo da fare è di ricavare M dalla formula precedente. Quindi si può ricavare E da M, e infine f da E, operazioni che un calcolatore elettronico esegue facilmente (benché una volta questi calcoli venivano svolti a mano, e non altrettanto facilmente e velocemente). La formula per r permette quindi di dedurre la posizione del satellite lungo la sua orbita. Tutto ciò che occorre per il calcolo sono gli elementi a, e e M(0), l'anomalia media al tempo t=0.