Centro di gravità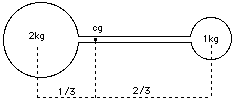

    Quasi tutti hanno almeno una nozione intuitiva del concetto di centro di gravità (CG), o baricentro, di un oggetto: è il punto nel quale un oggetto può stare perfettamente in equilibrio. Tenete una scopa per una estremità e l'altra estremità tenderà a cadere verso il basso; tenetela invece per il suo baricentro e la scopa resterà in equilibrio, e nessuna delle due estremità tenderà a inclinarsi verso il basso.

    Se avete imparato a tenere in equilibrio una sedia o una scopa sul palmo della vostra mano, sapete che il trucco è di tenere la mano esattamente sotto il centro di gravità. Poiché la mano non sta nel centro di gravità, ma al di sotto, occorre continuamente muoverla per mantenerla in quella posizione strategica.

    Esiste anche una precisa definizione matematica, che non ha niente a vedere con la gravità, ed è questo il motivo per cui molti scienziati ed ingegneri preferiscono il termine centro di massa. Tuttavia questo discorso ci porterebbe lontano, e non è il caso di trattarlo qui. Una leggera asta con due sfere di uguale peso alle estremità ovviamente ha il suo CG nel suo punto medio. Quando però una delle due sfere pesa il doppio dell'altra, il CG si trova a una distanza proporzionale al rapporto 1:2, dalla parte della sfera più pesante (ved. la figura in alto). E similmente per altri rapporti.

Sfere che si respingono tra loro

    Immaginiamo ora che le due sfere, anziché da un'asta leggera, siano collegate da una molla, tenuta compressa da una corda. Anche se le due sfere sono separate, si può ugualmente parlare di un loro comune centro di gravità, situato lungo la linea che congiunge i due centri, a un terzo della distanza dal centro della sfera più pesante.

    (Il centro di gravità del sistema Terra-Luna può essere definito nello stesso modo. Poiché il rapporto delle masse dei due corpi è di circa 81:1, il CG è il punto lungo la linea tra i due centri che la divide in tale rapporto. Si può dimostrare che -- trascurando l'attrazione del Sole e degli altri pianeti -- la Luna non orbita attorno al centro della Terra, ma piuttosto attorno al comune CG, e allo stesso modo si comporta la Terra, reagendo all'attrazione lunare. Naturalmente, poiché la Terra ha una massa molto maggiore, il CG non è molto lontano dal centro della Terra -- in effetti, si trova molto più vicino al centro che alla superficie della Terra).

    Supponiamo adesso di bruciare con un fiammifero la cordicella che tiene compressa la molla. Mentre questa si espande, spinge le due sfere all'esterno, e se la molla è abbastanza leggera, il suo moto non ha importanza e possiamo assumere che le sfere si respingano tra loro.

    Secondo la formulazione di Mach delle equazioni del moto, se la sfera più pesante riceve un'accelerazione a, allora l'altra sfera più leggera riceve un'accelerazione doppia, per cui, in ogni istante di tempo, la sua velocità totale, come pure la distanza percorsa, sarà il doppio di quella della sfera più pesante. La conservazione della quantità di moto porta allo stesso risultato.

    Se quindi la sfera pesante si trova a una distanza D dalla posizione iniziale della molla, la sfera più leggera si troverà a una distanza 2D, come nella prima figura, riportata all'inizio della pagina. Qualunque sia il tempo trascorso, il centro di gravità resta sempre nella stessa posizione.

I razzi

    Tutto questo è legato a un principio molto generale: in ogni oggetto o sistema di oggetti, le forze che agiscono solo su quegli oggetti e non su altri ("forze interne") non possono spostare il centro di gravità.

    Un astronauta che "galleggia" nella sua tuta spaziale non può cambiare la sua posizione senza far intervenire qualcos'altro, per esempio dando una spinta alla parete dell'astronave. Il centro di gravità -- o "centro di massa" -- è un punto fisso, che non può essere spostato senza un aiuto esterno (tuttavia è possibile ruotare attorno ad esso).

    Lanciando un oggetto pesante in una direzione, l'astronauta riesce a muoversi nella direzione opposta, anche se il comune centro di gravità resta sempre nella stessa posizione. Tenendo in mano una bomboletta di ossigeno compresso, si può ottenere lo stesso risultato spruzzando un getto di gas (una scena che appariva nei primi film di fantascienza). Un razzo fa esattamente la stessa cosa, tranne che il gas freddo è sostituito da un getto molto più violento di gas incandescente prodotto dalla combustione di un opportuno propellente.

Lancio di un   Atlas-Centaur.

    I potenti razzi che sollevano centinaia o anche migliaia di tonnellate dalla piattaforma di lancio sono basati sullo stesso principio. Se avete osservato un razzo che viene lanciato da Cape Canaveral, vale la pena di riflettere sul fatto che, se in qualche modo si togliessero dalla scena la piattaforma di lancio, l'atmosfera e la Terra, allora il comune centro di gravità del razzo e dei suoi gas combusti rimarrebbe sempre nel punto iniziale, cioè fermo sulla piattaforma di lancio.

Può sembrare un modo un po' tortuoso per produrre il moto, tuttavia i razzi sono (almeno per ora) l'unico modo pratico per lasciare la Terra e volare nello spazio.

--------------------------

   Nota: Buona parte dei paragrafi precedenti sono stati scritti per una versione iniziale del sito "Dagli astronomi...", per evitare l'uso esplicito della conservazione della quantità di moto. In seguito è stata aggiunta la sezione Imoment.htm sulla conservazione della quantità di moto, con annesso il programma della lezione ILmoment.htm. I paragrafi che seguono sono stati copiati dal file "ILmoment.htm", dove sono presentati come un'aggiunta facoltativa.

Il moto di un razzo

   [Il calcolo di questa "velocità media" è in realtà piuttosto complesso. Supponiamo che una certa massa m del getto sia espulsa con una velocità v. All'inizio, essa possiede una quantità di moto mv uguale e opposta a quella del razzo. Tuttavia, man mano che il razzo acquista velocità, occorrerebbe sottrarre tale velocità dal valore v, che era relativo alla posizione del razzo, il quale nel frattempo procede in avanti. Chiaramente, l'effetto del razzo diventerebbe sempre meno efficiente!

   Per evitare questo controsenso (il calcolo completo richiede nozioni di analisi matematica), definiamo una velocità media V dalla conservazione della quantità di moto, senza cercare di arzigogolare sulla sua relazione con la velocità v del getto. All'accensione, diciamo, il getto ha impartito una quantità di moto MV al carico utile, la quale è uguale e opposta a quella dei gas espulsi.]

   Il carico utile ha ora acquistato una velocità V.

Ma ne abbiamo bisogno di una maggiore! Pertanto, costruiamo un razzo di massa 4M, di cui 2M è il propellente, mentre il carico utile, anch'esso di massa 2M, è il razzo più piccolo descritto prima, che servirà come secondo stadio. Quando il propellente del razzo più grande è finito, e si è raggiunta una velocità V, si accende il secondo stadio, aggiungendo così una ulteriore velocità V, per un totale di 2V.

   Ancora più veloce! Adesso il razzo ha una massa 8M di cui 4M à il propellente del primo stadio, mentre 4M à il razzo che costituiva il razzo a due stadi del progetto precedente. Il primo stadio fornisce una velocità V, a cui gli altri due aggiungono il valore 2V, per un totale di 3V.

Ormai è chiaro l'andamento. Se la massa del carico utile finale è M, allora

Ogni volta che la velocità aumenta di una "tacca", la massa raddoppia.

   Non si può evitare questo genere di cose eliminando la struttura a stadi -- diciamo, in un razzo di massa 8M, accendendo tutta insieme la massa 7M di propellente. Questo poiché (come si è già notato), quando il carico utile (+ il restante propellente) guadagna velocità, è sempre minore la quantità di moto trasferita, in quanto il getto deve prima superare il movimento in avanti. In effetti, il calcolo corretto (che usa l'analisi infinitesimale) considera un numero enorme di piccoli stadi, accesi uno dopo l'altro. Si ottiene così ancora lo stesso risultato esponenziale.

   Questo è uno dei grandi problemi dell'astronautica, specialmente con il primo stadio che si deve alzare da terra: anche un piccolo carico utile richiede un razzo enorme. Forse un giorno gli esploratori dello spazio saranno in grado di eliminare un po' di peso di propellente, usando razzi alimentati ad aria ("scramjets") ma tale soluzione sembra attuabile soltanto per la parte più bassa (il primo quarto o il primo terzo) della velocità orbitale. Lanciare il razzo da un aereo in volo ad alta quota -- come lo "SpaceshipOne" di Burt Rutan, o il razzo a propellente solido "Pegasus", usati per mettere in orbita piccoli satelliti -- è anche un buon sistema per ridurre l'attrito atmosferico, che pure è un altro problema. Ma non ci sono altre scorciatoie in vista. Naturalmente, una volta in orbita, vi sono altri modi, più efficienti ma più graduali, per generare una buona spinta, come la propulsione a ioni.

-----------------------------------------------------
Domande poste dagli utenti:   Perché i razzi ruotano su se stessi?
                Un'altra domanda:  La forma dei razzi e delle astronavi.