(E27) Electro-Magnetic Waves, at last!
James Clerk MaxwellJames Clerk Maxwell was born 1831 in Edinburgh, Scotland, in the year when Faraday discovered electromagnetic induction. His father was a well-to-do attorney, but his mother died when he was young leaving him the only surviving child in the family. He studied in the Edinburgh Academy, a bright lad with interest and talent not only in mathematics and sciences, but also in drawing and poetry. Later he attended the Universities of Edinburgh and Cambridge, and from early age conducted original research and published articles. In 1856 he joined the faculty at Marischal (later the University of Aberdeen) and in 1860 moved to Kings College in London, where he got to know Faraday and appreciated his work.Faraday's grasp of physics was intuitive, without higher math. Maxwell had both math and the intuition, and he therefore tried to understand Faraday's vision and translate it into mathematical terms. He did much more in his short career (he died of cancer at 48), such as investigation into the theory of color and in particular the theory of gases. An ideal gas may be viewed as a collection of individual molecules moving randomly, with an average speed that increases with temperature, colliding elastically and frequently. Because of these collisions, some molecules gain energy above the average, others lose it, creating an average distribution found by Maxwell and still named the Maxwellian distribution. From his theory he deduced the viscosity of gases, the mean path of their molecules between collisions, and many other properties. He even worked out the theory of the radiometer, a vertical "windmill" with vanes black on one side and white on the other, spun up in an evacuated glass bulb by a beam of light. The spin is often attributed to light pressure, but the effect actually involves the residual gas inside the bulb and is much more subtle. Electric and Magnetic Fields, and Maxwell's EquationsHis greatest success, though, were "Maxwell's Equations"of electro-magnetism, a set of rigorous mathematical relations confirming Faraday's guess that a transverse electro-magnetic wave could exist, and that light is probably such a wave. He assembled the equations of electricity and magnetism--the basic ones which did not depend on properties of materials, but held even in a vacuum:
Maxwell expressed each of these statements in a suitable mathematical form, but we skip that part since it requires tools of differential calculus of three-dimensional quantities and of vectors. Number #2 is true even though we do observe magnetic poles on bar magnets, since the existence of such paired poles can also be explained by a suitable distribution of currents. It was Ampére who originally pointed out that if each atom included a small circulating current ("Ampére current"), lining up the axes of those currents would produce the same bulk magnetism as observed in bar magnets and lodestones. When #2 is formulated mathematically, its alternative interpretation is that magnetic field lines behave like streamlines in an incompressible fluid (like water, in practice; see discussion of magnetic flux). There remains a certain vagueness in all this: which here are "real" objects and which just mathematical abstractions? Electric charges and electric currents are presumably real, associated with the matter in which they reside--and if isolated magnetic poles existed, they might be deemed "real" too.
On the other hand the "electric force" and the "magnetic force" at a point in empty space seem somewhat abstract: unless an electric charge or electric current are actually located at such a point, it did not seem any different from any point in empty space. And yet Maxwell ultimately held that space without matter was not quite empty. A point associated with a possible electric force was endowed with an "electric field E," a vector with strength and direction, implying that if a charge q was placed there, it would sense a force qE. Similarly, an otherwise empty point would be endowed with a magnetic field B if a force mB would be sensed by a magnetic pole m there, if such poles existed--or a force I(dlxB) on a current I in a short length of conductor dl (a vector), as explained at the end of The Displacement CurrentWaves in general are associated with a periodic interchange of energy:
The two were linked, but a gap seemed to exist. By equation (4), varying the magnetic field B changes the magnetic flux, producing a changing electric field E. If a transformer is placed amid the changing flux, this E will create in its coil a changing current I, which may create more of the variable magnetic field B. But a changing current I is essential. If no coil is placed in that space, no current is expected, and current is what creates a magnetic field B. A changing electric field E was not seen as a source of magnetism. Except..... for that strange way an AC current can flow across a capacitor, even if the space between the plates is empty. Given two parallel plates A and B, if the voltage at A changes, for the short interval before the charge (and energy) of the capacitor can change, the voltage at B follows the one on A. At least for that very short time, a voltage change does propagate across the gap, as is demonstrated in AC currents. There, if the input is an AC voltage with angular frequency ω, the current flowing across the gap is proportional to ω, too. The frequency f associated with a light wave can be calculated from its wavelength λ in optical experiments and from the velocity of light c: f=c/λ One gets quite high frequencies, at which this unusual AC current crossing the gap of a capacitor might cross empty space quite easily. Maxwell named it the displacement current, represented by an added term in Maxwel's 4th equation. Does the displacement current have the same properties as current conducted by a wire--in particular, is it able to create a magnetic field B? Maxwell guessed it did, and so a high frequency AC electric field E could drive a high frequency AC magnetic field B across empty space. Equations could then be written in which a wave of E and one of B alternate, perpendicular to each other and (for both) to the direction in which the wave advances ("the ray of light"), with a velocity which in vacuum equals c. In ordinary light E can be in any direction perpendicular to the ray, but polarized waves, where (say) E is always in the same direction (and B perpendicular to it) are also possible
The FulfilmentIn 1884 John Henry Poynting proved that if electro-magnetic waves existed, they would be able to transmit both energy and momentum to material which intercepted them, which seemed a valid test of their reality. The energy is evident in any object heated by bright sunlight, and the momentum showed itself in the pressure of sunlight measured in 1902 by Lebedev in Russia. It is now considered for solar sails in deep space. Maxwell died of stomach cancer in 1879, and who knows what else he may have contributed, had he lived to a ripe old age. One important question remained: how could an electromagnetic wave be generated? Its details occupied many scientists in the 50-60 years that followed and led to an entire new insight on physics at the atomic scale, now known as quantum theory. Hot solid substances radiated a continuous spectrum whose frequency rose with energy--from cherry-red hot iron in a smith's forge, to the bright yellow light of the filaments of Edison and Welsbach--to the even hotter electric arc of Humphry Davy, whose light contained a lot of ultra-violet (the reason arc welders wear special masks). The hotter the source, the shorter the wavelength, but for a while scientists did not understand why. Glowing gases (e.g. in fluorescent lights) behaved differently. When excited by high voltages, they preferred to emit light at selected frequencies ("line spectrum"), accurately defined and characteristic of the emitting substance. Here was clearly a lot of information, and it took a complete overhaul of physics to figure it out; see here, here and here for some details. All these involved processes on an atomic scale, where electro-magnetic circuitry does not exist and where (as it turned out) laws of physics are markedly modified. But how to create electromagnetic waves using known electrical equipment in the laboratory? Heinrich Hertz in Germany proved mathematically and confirmed by experiment in 1886 that the high-frequency AC in a loop antenna (generating a magnetic field) or an antenna composed of two opposing rods (a "dipole antenna," with the circuit closed by the displacement current) could generate an E-M wave. It was already known that lightning and sparks produced currents which oscillated very rapidly, a mixture of high-frequency AC (even now, on an AM radio during a thunderstorm, you can hear the crackling of "static" due to lightning, regardless of the station you are tuned to). 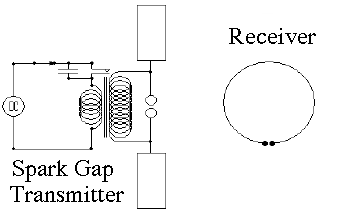
Hertz created a high frequency spark discharge by using a transformer to generate a high voltage and discharging it through an "antenna" (he tried both kinds) with a spark gap in the middle (see also here). The oscillations between a charged capacitor and an inductor can also broadcast an E-M wave. Hertz was mainly interested in proving the generation of electromagnetic waves; little did he suspect that by 1903 Marconi would send radio signals across the Atlantic ocean, or that in 1912 the sinking "Titanic" would radio for help after colliding (at full speed) with a drifting iceberg. |
|
Next Stop: E28. Communication
Home Page "All Things Electric and Magnetic"
Author and Curator: Dr. David P. Stern |

