(11a) Le ellissi e la prima legge di Keplero
|
Come avevamo già accennato, esistono altri modi per individuare un punto su un piano. Per esempio, un punto P può essere specificato dalla sua distanza r da un punto centrale O ("origine") e dall'angolo φ (la lettera greca "phi") che la linea OP forma con qualche direzione di riferimento. Queste "coordinate polari" (ved. il disegno in basso a destra) sono il mezzo più adatto per descrivere il moto planetario. L'ellisse in coordinate polariDi nuovo, se tutti i valori di (r,φ) di una curva sono correlati da una qualche equazione che può essere simbolicamente scritta r = r(φ) allora la funzione r(φ) si chiama l'equazione della curva, in coordinate polari. La funzione più semplice è un numero costante a, a cui corrisponde la curva r = a 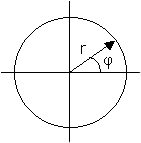
Il valore di r è uguale ad a per ogni valore di φ. Si ha in tal caso una circonferenza con centro nell'origine e di raggio uguale ad a, mostrata nella figura qui a destra. L'ellisseConsideriamo adesso la curva di equazione r = a(1– e2)/(1+ e cos φ) dove l'eccentricità e è un numero compreso tra 0 e 1. Se e = 0, torniamo chiaramente al caso della circonferenza esaminata qui sopra. Ma che succede per valori diversi? La funzione cos φ ha un comportamento ondulatorio (ved. l'immagine qui sotto), e, al variare di φ lungo tutta la circonferenza, passa prima da +1 a 0, poi al valore –1, e infine di nuovo a 0 e a +1. Anche il denominatore cresce e diminuisce con andamento ondulatorio, ed ha un minimo quando cos φ = –1. Sotto alla figura è riportata una tabella con i valori principali della funzione (360 sta tra parentesi, poiché rappresenta la stessa direzione di 0 gradi): 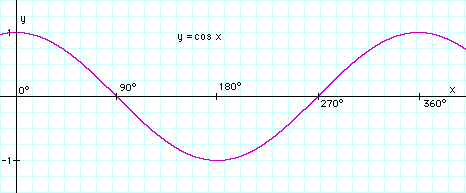
|
| φ in gradi | 0 | 90 | 180 | 270 | (360) |
| cos φ | 1 | 0 | –1 | 0 | 1 |
| 1 + e cos φ | 1 + e | 1 | 1 – e | 1 | 1 + e |
|
Fintantoché e è minore di 1, il denominatore è positivo. Non è mai zero, per cui, qualunque sia il valore di φ, si potrà sempre trovare un corrispondente valore di r. In altre parole, la curva gira completamente attorno all'origine ed è chiusa. L'espressione (1 – e2) può essere scomposta in fattori, cioè scritta come due espressioni moltiplicate tra loro ("il prodotto di due espressioni"). Come viene discusso nella sezione sulle identità algebriche 1 – e2 = (1 – e)(1 + e) Per qualcuno dei punti della tabella precedente, (1 – e) oppure (1 + e) fa annullare il denominatore, dando: |
| φ in gradi | 0 | 90 | 180 | 270 | (360) |
| r | a(1 – e) | a(1 – e2) | a(1 + e) | a(1 – e2) | a(1 – e) |
|
La distanza di un punto della curva dall'origine fluttua quindi tra a(1 – e) e a(1 + e), e il risultato è una circonferenza schiacciata o ellisse; il punto O (l'origine) è il suo fuoco. Tutte le orbite planetarie rassomigliano ad ellissi, ciascuna con un suo valore di e o eccentricità: più è piccolo il valore di e, e più la forma si avvicina a quella di una circonferenza. L'orbita terrestre è quasi circolare, con una eccentricità e = 0,0168, e gli altri pianeti maggiori (eccetto Plutone) hanno eccentricità simili: se guardaste un disegno in scala delle orbite tracciate su un foglio di carta, non riuscireste a vedere a occhio che non si tratta di circonferenze. L'orbita della cometa di Halley, al contrario, ha una eccentricità molto prossima a 1. |
| Come menzionato nella precedente sezione vi è un secondo fuoco O' in posizione simmetrica rispetto ad O, e l'ellisse può essere definita (che è poi la sua definizione originale) come l'insieme dei punti per cui la somma R1+R2 delle loro distanze da O e da O' è sempre la stessa.
La dimensione maggiore dell'ellisse, cioè il segmento AB lungo la linea che congiunge i fuochi, è detto "asse maggiore". Supponiamo che (R1,R2) siano le distanze di A dai fuochi O e O'. Allora R1 = OA = a(1–e) è la minima distanza della curva da O, mentre R2 = O'A = OB (per simmetria) è la massima distanza, che quindi è uguale a |
|
|
Il prossimo argomento: #12 La seconda legge di Keplero
Cronologia Glossario Torna alla pagina iniziale
Autore e Curatore: Dr. David P. Stern
Ci si può rivolgere al Dr. Stern per posta elettronica (in inglese,
per favore!):
stargaze("chiocciola")phy6.org
Traduzione in lingua italiana di Giuliano Pinto
Aggiornato al 10 Dicembre 2005

