Note: I formati disponibili nelle pagine Web richiedono che le frazioni siano indicate con una barra (/). Può essere una buona idea copiare le espressioni matematiche (via via che le incontrate) su un foglio di carta, e rappresentare le frazioni usando le normali linee di frazione, così da avere delle espressioni più familiari.

   Indichiamo la costante gravitazionale con G, la massa del Sole con M, quella della Terra con m, la distanza della Terra dal Sole con r e la sua velocità orbitale con v. Applicando quanto si è detto sulla gravità e sulle forze centripeta e centrifuga, si ottiene (come nella sezione 20)

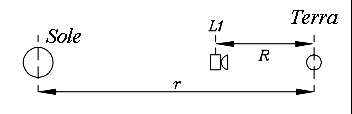
  Consideriamo ora un'astronave di massa m_ast , posizionata sulla linea che congiunge la Terra con il Sole, a una distanza R dalla Terra e a una distanza (r–R) dal Sole (ved. disegno). La forza F che l'attrae verso il Sole è diminuita dall'attrazione della Terra in direzione opposta, per cui

  Supponiamo che anche questa astronave si muova in un'orbita circolare attorno al Sole, con una velocità v_ast . Allora, se la forza centrifuga controbilancia l'attrazione (o meglio, l'attrazione fornisce la forza centripeta)

In modo simile al calcolo precedente, moltiplichiamo entrambi i membri per (r–R)/m_ast , ottenendo

Assumiamo che anche l'astronave si muova attorno al Sole in un'orbita circolare di raggio (r–R). (Questo naturalmente richiede che la Terra sia sempre in una posizione tale da esercitare un'attrazione in direzione opposta al Sole, ma torneremo fra breve su questo argomento). Il periodo orbitale T_ast  del satellite soddisfa quindi, come precedentemente

oppure, dividendo tutto per (r–R)²

Questa espressione rassomiglia alla precedente equazione della "Terza legge", tranne che per il fatto che ora abbiamo aggiunto il termine corrispondente all'attrazione della Terra in direzione opposta. Ma la Terra sarà sempre in una posizione tale da esercitare la sua attrazione sull'astronave in direzione esattamente opposta al Sole? No, a meno che i due periodi orbitali siano identici:

Soltanto in tale caso il moto dell'astronave è sincronizzato con quello della Terra e la distanza tra i due corpi resta costante. Questo in genere avviene soltanto per un valore di R, cioè soltanto per una certa distanza dalla Terra, e tale distanza, R, è proprio il valore incognito che dobbiamo ricavare, la "cosa" che stiamo cercando. Se T_ast  = T, le due relazioni con 4π²/T² a secondo membro sono uguali tra loro, fornendo così un'equazione da cui è possibile ricavare R. Questa equazione è

  Dividiamo entrambi i membri per GM: allora G sparisce dalla scena, e, al posto delle masse (m, M) di (Terra, Sole) abbiamo solo il loro rapporto, un piccolo numero che chiameremo y

oppure, con notazioni scientifiche (il punto indica moltiplicazione)

L'equazione è ora

Moltiplicando entrambi i membri per r³

In ciascuna delle frazioni, dividiamo numeratore e denominatore per r³ [Questo equivale a moltiplicare la frazione per (1/ r³)/(1/r³). Poiché ogni frazione che ha il numeratore uguale al denominatore è uguale a 1, questo è lo stesso che moltiplicare per 1, e quindi non si ha nessun cambiamento]. Inoltre, introduciamo una nuova variabile z, pari a R/r. Allora

  Adesso siamo pronti a ricavare la quantità incognita z. L'equazione precedente è un po' complicata -- in effetti probabilmente non esiste una formula esatta per la sua soluzione. Tuttavia, poiché z è piccolo, è abbastanza facile ottenere una soluzione approssimata, usando i metodi riportati nella sezione (M-5). Viene lì mostrato che

Sostituendo queste approssimazioni nell'equazione principale si ottiene

  Tutti e due i membri di questa relazione sono ora ugualmente piccoli. Il secondo membro è stato modificato solo leggermente con l'aggiunta di z: possiamo quindi trascurare questo termine senza che ne derivi una grande differenza. Pertanto

  Così la distanza di L1 dalla Terra è di circa un centesimo della distanza del Sole. È ora possibile tornare sui nostri passi per ricavare delle equazioni più accurate, come 3z³ ~ y(1+z), e sostituire z a secondo membro con il suo valore approssimato 0,01, per ricavare quindi un valore più accurato. Questo procedimento di miglioramento progressivo, chiamato iterazione, viene usato anche per l'equazione di Keplero, discussa nella sezione (12a). A causa della piccolezza di z, questi raffinamenti cambieranno molto poco il valore finale.