Disclaimer: The following material is being kept online for archival purposes.

Although accurate at the time of publication, it is no longer being updated. The page may contain broken links or outdated information, and parts may not function in current web browsers.

Mappa del sito                                                                                                     Programma della lezione


(8b) La parallasse

Uso della trigonometria

  "Pre-Trigonometria"

La sezione M-7 descrive il problema fondamentale della trigonometria (ved. disegno in basso a sinistra): trovare la distanza di un certo punto lontano (C), conoscendo le direzioni sotto cui è visto C quando viene osservato dalle due estremità di una linea di base AB. Questo problema diventa un po' più semplice se:
  1. La linea di base è perpendicolare alla linea che va dal suo punto di mezzo all'oggetto lontano, cioè il triangolo ABC è isoscele. Indicheremo i suoi lati uguali con r:

    AC = BC = r

  2. La lunghezza c della linea di base AB è molto minore di r. Questo significa che l'angolo α tra AC e BC è piccolo. Questo angolo è chiamato la parallasse di C, vista da AB.

  3. Non chiederemo una grande precisione, ma saremo soddisfatti da un valore della distanza approssimato, diciamo, entro l'1%.
Il metodo presentato qui era già usato dagli antichi Greci più di 2000 anni fa. Essi sapevano che la lunghezza di una circonferenza di raggio r era 2πr, dove π (una notazione moderna, non quella dei greci, anche se π fa parte del loro alfabeto) indica un numero un po' più grande di 3, approssimativamente

π = 3,14159...

    (Il matematico siracusano Archimede derivò π con un'accuratezza di 4 cifre, anche se Archimede lo espresse in modo diverso, poiché le frazioni decimali apparvero in Europa solo 1000 anni più tardi).
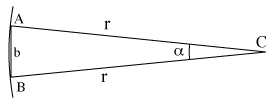
Tracciamo una circonferenza di raggio r attorno al punto C, passante per A e per B (ved. disegno sopra). Poiché l'angolo α è molto piccolo, la lunghezza della "linea di base" b rettilinea (ved. disegno a fianco, dove è stato dato un altro nome alla distanza AB) non è molto diversa dalla lunghezza dell'arco di circonferenza che passa per A e B. Assumiamo che le due lunghezze siano uguali (questa è l'approssimazione che facciamo qui). La lunghezza di un arco di circonferenza è proporzionale all'angolo al centro corrispondente, e poiché Un triangolo molto allungato
b corrisponde a un angolo    α
2π r corrisponde a un angolo di  360°

otteniamo

2π r = (360°/ α b)

e dividendo per 2π

r = (360°/2 π α) b

Quindi, se conosciamo b, possiamo ricavare r. Per esempio, se sappiamo che α = 5,73°, 2 π α = 36° ed otteniamo

r = 10 b

Valutazione di una distanza all'aperto

Il metodo descritto qui è utile per escursionisti ed esploratori. Supponiamo di volere stimare la distanza di un oggetto lontano, per esempio, un edificio, un albero o una torre idrica.

Il disegno mostra una rappresentazione schematica della situazione vista dall'alto (non in scala). Per stimare la distanza dell'oggetto A, si può seguire il seguente procedimento:

Metodo del pollice per stimare una distanza

  1.   Allungate il braccio in avanti ed estendete il pollice, con l'unghia rivolta verso i vostri occhi. Chiudete un occhio (A') e spostate il pollice in modo che, guardando con l'occhio aperto (B'), possiate vedere il pollice che copre l'oggetto A in questione.

  2.   Successivamente aprite l'occhio che prima tenevate chiuso (A') e chiudete quello (B') con cui guardavate prima, senza spostare il pollice. Vi sembrerà che il pollice si sia mosso: infatti non si trova più davanti all'oggetto A, ma davanti a un altro punto alla stessa distanza da voi, indicato con B nel disegno.

  3.   Fate una stima della distanza reale tra A e B, confrontandola con le altezze degli alberi, le dimensioni di un edificio, la distanza tra i tralicci dell'alta tensione, la lunghezza delle automobili, ecc. La distanza a cui si trova l'oggetto A da voi è 10 volte la distanza AB.
      E perché tutto questo? Poiché, anche se ogni persona ha una taglia diversa, le proporzioni del corpo umano sono in media piuttosto costanti, e per la maggior parte delle persone l'angolo tra le linee che vanno dagli occhi (A',B') al pollice con il braccio teso è di circa 6°, abbastanza vicino al valore 5,73°, da cui avevamo ricavato il rapporto 1:10 all'inizio di questa sezione.   Questo angolo è la parallasse del vostro pollice, visto dai due occhi. Il triangolo A'B'C ha le stesse proporzioni del triangolo molto più grande ABC (cioè i due triangoli sono simili), e quindi, se la distanza B'C fino al vostro pollice è 10 volte la distanza A'B' tra i due occhi, anche la distanza AC fino all'oggetto lontano è 10 volte la distanza AB.


   

Quanto è lontana una stella?

  Quando valutiamo la distanza di un oggetto molto lontano, è meglio che anche la nostra "linea di base" tra i due punti di osservazione sia molto lunga. Gli oggetti più lontani che i nostri occhi sono in grado di vedere sono le stelle, che effettivamente sono enormemente lontane: la loro luce, che viaggia a 300·000 chilometri al secondo, impiega anni, talvolta moltissimi anni, per arrivare fino a noi. La luce del Sole impiega 500 secondi a raggiungere la Terra, poco più di 8 minuti, e circa 5 ore e mezzo per raggiungere Plutone, il pianeta più lontano. Un "anno luce" è una distanza circa 1600 volte più grande, una distanza immensa.

  La più lunga linea di base che abbiamo a disposizione per misurare distanze così grandi è il diametro dell'orbita terrestre, 300·000·000 chilometri. Il moto della Terra attorno al Sole fa sì che essa si sposti avanti e indietro nello spazio, in modo che, a distanza di sei mesi, le sue posizioni distano di 300·000·000 chilometri l'una dall'altra. Inoltre, anche l'intero Sistema Solare si muove nello spazio, ma quel moto non è periodico, per cui i suoi effetti non sono separabili.

  E di quanto si spostano le stelle quando sono viste da due punti di osservazione lontani 300·000·000 chilometri l'uno dall'altro? In realtà poco, molto poco. Per molti anni gli astronomi hanno cercato invano di notare la differenza. Soltanto nel 1838 si poté misurare la parallasse di alcune delle stelle più vicine: per Alpha Centauri da Henderson dal Sudafrica, per Vega da Friedrich von Struve e per 61 Cygni da Friedrich Bessel.

  Tali osservazioni richiedono una estrema precisione. Un cerchio è diviso in 360 gradi (360°), ogni grado è diviso in 60 minuti (60') -- detti anche "minuti d'arco" -- e ogni minuto contiene 60 secondi d'arco (60"). Ora, tutte le parallassi osservate sono minori di 1", al limite della risoluzione anche dei più grandi telescopi terrestri.

  Nelle misure delle distanze stellari, gli astronomi usano spesso il parsec, che è la distanza di una stella, la cui parallasse sia pari a 1" -- un secondo d'arco. Un parsec è uguale a 3,26 anni luce, ma come si è detto, nessuna stella è così vicina. Alpha Centauri, la stella più vicina al Sistema Solare, dello stesso tipo del nostro Sole, si trova a una distanza di 4,3 anni luce, che corrispondono a una parallasse di 0,75".

  Alpha Centauri non è un nome, ma una designazione. Infatti gli astronomi designano le stelle in ogni costellazione con le lettere dell'alfabeto greco -- alfa, beta, gamma, delta, e così di seguito, e "Alpha Centauri" significa che si tratta della stella più luminosa della costellazione del Centauro, che si trova nel cielo australe. Occorre trovarsi a sud dell'equatore per poterla vedere bene.

Il prossimo argomento: #8c  Quanto è lontana la Luna?--1

            Cronologia                     Glossario                     Torna alla pagina iniziale

Autore e Curatore:   Dr. David P. Stern
     Ci si può rivolgere al Dr. Stern per posta elettronica (in inglese, per favore!):   stargaze("chiocciola")phy6.org

Traduzione in lingua italiana di Giuliano Pinto

Aggiornato al 21 Marzo 2005


Above is background material for archival reference only.

NASA Logo, National Aeronautics and Space Administration
NASA Official: Adam Szabo

Curators: Robert Candey, Alex Young, Tamara Kovalick

NASA Privacy, Security, Notices