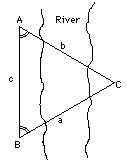
Il problema di base della trigonometria si presenta grossomodo così:

Vi trovate presso un grande fiume e avete la necessità di conoscere la distanza attraverso di esso – diciamo fino ad un albero sull'altra riva, indicato sul disegno qui a lato dalla lettera C (per semplicità, ignoriamo la terza dimensione). Come lo si può fare senza attraversare addirittura il fiume?

Il tipico modo di procedere è il seguente. Piantate due paletti nel terreno nei punti A e B, e con un metro a nastro o con una catena da geometra misurate la distanza c tra loro ("la linea di base").

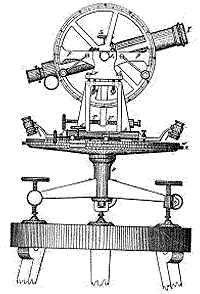
Quindi rimuovete il paletto in A e sostituitelo con un cannocchiale da geometra come quello mostrato qui ("teodolite"), con una piastra circolare divisa in 360 gradi, che indicano la direzione ("azimuth") in cui il cannocchiale sta puntando. Puntando il cannocchiale, prima sull'albero e poi sul paletto B, misurate l'angolo A del triangolo ABC, uguale alla differenza tra i numeri che avete letto dalla piastra azimutale. Ripiantate il paletto, portate il vostro cannocchiale nel punto B e misurate l'angolo B nello stesso modo.

La lunghezza c della base, e i due angoli A e B, contengono tutto ciò che c'è da sapere sul triangolo ABC – abbastanza, per esempio, per costruire un triangolo della stessa dimensione e forma su un opportuno campo aperto. La trigonometria (trigon = triangolo) era in origine l'arte di trarre le informazioni mancanti mediante puro calcolo. Date sufficienti informazioni per definire un triangolo, la trigonometria permette di calcolare le dimensioni e gli angoli rimanenti.

Perché triangoli? Perché sono i mattoni di base dai quali ogni forma (con confini rettilinei) può essere costruita. Un quadrato, un pentagono o un altro poligono possono essere divisi in triangoli, diciamo da linee rette che si irradiano da un angolo a tutti gli altri.

    Nel mappare un paese, i geometri lo dividono in triangoli e marcano ogni angolo con un "riferimento", che oggi è spesso una piastra circolare di ottone infissa nel terreno, con un una concavità al centro, sulla quale i geometri piazzano le loro aste e cannocchiali (George Washington ha fatto questo tipo di lavoro da adolescente). Dopo aver misurato la linea di base – nell'esempio del fiume – il geometra dovrebbe misurare (come descritto qui) gli angoli che essa forma con le linee dirette verso un certo punto C e usare la trigonometria per calcolare le distanze AC e BC. Queste possono servire come linee di base per ulteriori triangoli, ciascuno dei quali fornisce linee di base per ulteriori due ... e così via, sempre più triangoli triangoli finché tutto il paese è coperto da una griglia che contiene solo distanze conosciute. Più tardi può essere aggiunta una griglia secondaria, suddividendo i triangoli più grandi e marcando i suoi punti con pali di ferro, fornendo ulteriori distanze note su cui tutte le mappe e piante possono essere basate.

   

    Un largo progetto di agrimensura del 1800 fu la "Great Trigonometric Survey" (Grande Agrimensura Trigonometrica) dell'India Britannica. Per la realizzazione del progetto furono realizzati i due teodoliti più larghi di sempre, dei mostri con scale circolari di ampiezza 36 pollici (91,44 centimetri), sulle quali le impostazioni venivano lette con una eccezionale accuratezza mediante 5 microscopi. Ciascuna nella propria custodia pesava mezza tonnellata e richiedeva 12 uomini per trasportarla. Con esse, il progetto coprì il paese con svariate stringhe di triangoli nelle direzioni nord-sud e est-ovest (le aree tra le stringhe furono lasciate per dopo) e ci vollero decenni per essere portato a termine.

    Nota: I dettagli sulla scoperta del Monte Everest e l'agrimensura dell'India sono presi da "Who Discovered Mount Everest?" (Chi ha scoperto il Monte Everest?) di Parke A. Dickey, Eos (Transactions of the American Geophysical Union), vol 66, pp. 697-700, 8 Ottobre 1985. L'articolo è ristampato alle pp. 54-59 della History of Geophysics, (Storia della Geofisica) Vol. 4, edita da C. Stewart Gillmor, pubblicata dalla American Geophysical Union (Unione Geofisica Americana), 1990.

    Un resoconto molto leggibile, compresa la storia di William Lambton, il fautore di quella misurazione, può essere trovata in "The Great Arc : The Dramatic Tale of How India Was Mapped and Everest Was Named" (Il grande arco: l'entusiasmente storia di come l'India fu cartografata e l'Everest fu chiamato così) di John Keay, 160 pagine copertina rigida, Harper and Collins, Settembre 2000.