|
|
|
|
|
|
|
|
(M-9) Come Ricavare i Seni e i Coseni
|
Ricavare il seno o il coseno di un angolo arbitrario richiede un pò più matematica di quanta sia discussa qui. Tuttavia, ricavarli per alcuni angoli speciali è relativamente semplice. Angoli complementariSi noti prima di tutto che un triangolo rettangolo contiene due angoli. Dal momento che la somma di tutti e tre gli angoli (in ogni triangolo) è di 180°, la somma dei due angoli acuti è di 90°. Ne consegue che se uno degli angoli è di A gradi, l'altro (il suo "angolo complementare") è (90° − A). Il seno e il coseno sono stati definiti come i seguenti rapporti: sen A = (lato opposto ad A)/(lato lungo) Siccome il lato opposto ad A è quello adiacente a (90° − A), ne consegue che il seno di un angolo è il coseno dell'altro, e viceversa: sen A = a/c = cos (90° – A) Questo è un grande aiuto: il calcolo (per esempio) del seno e del coseno di 30°ci dà anche, come bonus, il seno e il coseno di 60°. (1) A = 45°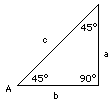 Se A = 45°, quindi anche (90° – A) = 45°, e perciò
Se A = 45°, quindi anche (90° – A) = 45°, e perciò
sen2 45° = 1/2
sen 45° = √2/√4 = √2/2
(2) A = 30°, (90° – A) = 60°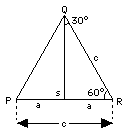 Si consideri il triangolo PQR (disegno) con tutti e tre gli angoli uguali a 60°. Per simmetria, anche tutti e tre i lati sono uguali (esiste una dimostrazione più rigorosa, ma la saltiamo). Disegnamo una linea QS perpendicolare a PR: essa divide l'angolo grande in due triangoli rettangoli con angoli acuti di (30°, 60°), che è il genere che ci interessa. Per simmetria, i triangoli sono di uguale dimensione e forma ("congruenti") e perciò (saltando un'altra dimostrazione)
Si consideri il triangolo PQR (disegno) con tutti e tre gli angoli uguali a 60°. Per simmetria, anche tutti e tre i lati sono uguali (esiste una dimostrazione più rigorosa, ma la saltiamo). Disegnamo una linea QS perpendicolare a PR: essa divide l'angolo grande in due triangoli rettangoli con angoli acuti di (30°, 60°), che è il genere che ci interessa. Per simmetria, i triangoli sono di uguale dimensione e forma ("congruenti") e perciò (saltando un'altra dimostrazione)
Nella notazione del disegno
a/c = 1/2 = sen 30° = cos 60°
Sottraendo 1/4 da ambo i membri
cos 30° = √3/ √4 = (√3)/2 = 1.7320508/2 cos 30° = 0.8660254 = sen 60°
(3) A = 90° , (90° – A) = 0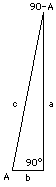 Sarebbe piuttosto difficile disegnare un triangolo rettangolo con un secondo angolo di 90° al suo interno, perchè il terzo angolo dovrebbe allora essere di 0°. Ma possiamo immaginare questo strano triangolo come il caso limite di triangoli lunghi e stretti con un angolo A che è molto ampio e il suo complemento (90° – A) molto piccolo (disegno). Nel caso limite
Sarebbe piuttosto difficile disegnare un triangolo rettangolo con un secondo angolo di 90° al suo interno, perchè il terzo angolo dovrebbe allora essere di 0°. Ma possiamo immaginare questo strano triangolo come il caso limite di triangoli lunghi e stretti con un angolo A che è molto ampio e il suo complemento (90° – A) molto piccolo (disegno). Nel caso limite
cos A = b/c = 0 e perciò 1 = sen2A + cos2A = sen2A + 0 ne consegue che sen2A = 1 sen A = 1 Perciò cos 90° = sen 0° = 0 La tabella completa quindi mostra |
| A | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| sin A | 0 | 0.5 | 0.707107 | 0.866025 | 1 |
| cos A | 1 | 0.866025 | 0.707107 | 0.5 | 0 |
|
Dovreste essere in grado di disegnare un grafico abbastanza buono di senA e cosA utilizzando i punti di cui sopra (4) Postlaurea: A = 15°, (90° – A) = 75°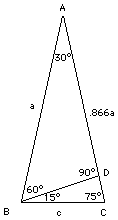
I calcoli e la tabella precedenti sono argomenti di base praticamente in ogni corso o testo di trigonometria. Potete osservare tuttavia gli intervalli tra 0° e 30°, e tra 60° e 90°. Se vogliamo che l'angolo A cresca a intervalli uguali di 15°, abbiamo ancora bisogno del seno e del coseno di 15° e 75°. Siete interessati? Ecco come può essere fatto; tenete a portata di mano la vostra calcolatrice! Disegnate il triangolo ABC, con l'angolo A uguale a 30° e i due angoli alla base uguali entrambi a 75°. Quindi disegnate la linea BD perpendicolare ad AC (si veda il disegno sulla destra). Per simmetria, i lati AB e AC sono della stessa lunghezza; si indichi tale lunghezza con la lettera a. Il triangolo ABD ha angoli di 90, 60 e 30 gradi, ed è perciò del genere esaminato prima. Abbiamo BD = a sen 30° = 0.5 a Quindi DC = AC – AD = a – 0.866025 a = 0.133975 a 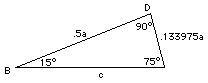 Ora guardate il triangolo BDC: i suoi due angoli più grandi sono uguali a 90° e 75°, forzando l'angolo rimasto ad essere uguale a 15°. Usando il teorema di Pitagora, se il lato lungo è chiamato c, abbiamo
Ora guardate il triangolo BDC: i suoi due angoli più grandi sono uguali a 90° e 75°, forzando l'angolo rimasto ad essere uguale a 15°. Usando il teorema di Pitagora, se il lato lungo è chiamato c, abbiamo
BD2 + CD2 = c2 = (0.5 a)2 + (0.133975 a)2 Facendone la radice quadrata c = 0.517638 a Da essa, fermandoci ai 5 decimali (e considerando anche l'angolo complementare di 75°) sen 15° = 0.133975/0.517638 = 0.25882 = cos 75° Ora andate a disegnare il vostro grafico! |
Prossimo Argomento: #M-10 Andando Oltre i 90 Gradi
Autore e Curatore: Dr. David P. Stern
Ci si puņ rivolgere al Dr. Stern per posta elettronica (in inglese, per favore!):
stargaze("chiocciola")phy6.org
Traduzione in lingua italiana di Pietro Sauro
Aggiornato al 25 Novembre 2001
