|
|
|
|
|
|
|
|
(M-12) La Tangente
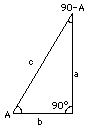 La tangente è uno strumento di trigonometria, legato al seno e al coseno. In questo sito web è usato in connessione alla balestriglia.
La tangente è uno strumento di trigonometria, legato al seno e al coseno. In questo sito web è usato in connessione alla balestriglia.Sapete già che i triangoli rettangoli sono fondamentali per la trigonometria. Sia ABC un triangolo di questo tipo (disegno) con C = 90° l'angolo retto e (A, B) gli angoli acuti. Inoltre, siano a, b e c le lunghezze dei suoi tre lati – a quella del lato opposto ad A, b di quello opposto a B, e c quella più lunga, opposta a C. Due utili rapporti associati all'angolo A ("funzioni trigonometriche di A") sono
Entrambi questi rapporti contengono il lato lungo c ("ipotenusa" in gergo matematico), e siccome sia a che b devono essere più piccoli di quel lato, questi rapporti sono sempre numeri minori di 1. Ora aggiungiamo due ulteriori rapporti alla nostra collezione – la tangente e la cotangente: La tangente di A E la cotangente di A
Si moltiplichi numeratore e denominatore per c (è lo stesso che moltiplicare la frazione per (c/c)=1) e si ottiene
Le calcolatrici che danno i seni e i coseni, e i libri che tabellano i loro valori, sono anche in grado di fornire le tangenti e le cotangenti.
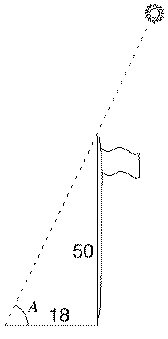
Una Semplice ApplicazioneA mezzogiorno un pennone verticale di altezza 50' (50 piedi) ha un'ombra lunga 18 piedi. Quanto vale l'angolo A che il Sole forma rispetto all'orizzonte? (Come spiegato nella sezione "Navigazione, " quell'angolo permette di calcolare la latitudine della propria posizione.) Dal disegno:
Se avete una tabella delle tangenti, ora potete cercare gli angoli le cui tangenti sono appena al di sopra e appena al di sotto di quel valore, e stimare dove, tra loro, dovrebbe trovarsi A ("interpolazione"). Le calcolatrici generalmente hanno un tasto "tan" che, una volta inserito l'angolo, fornisce la tangente. Ma molte di esse hanno anche un tasto "tan -1 " che fa il contrario – data la tangente, tira fuori l'angolo. (Il tasto può essere lo stesso che permette di calcolare tan-1 se prima si preme un tasto "modalità speciale" colorato; tan-1 è chiamata anche "inversa della tangente" o "arcotangente"). In questo esempio,
P.S.: Una tangente ad una circonferenza è una linea che la tocca in un solo punto. Se mai vi foste chiesti come mai il nome "tangente" è stato introdotto in trigonometria, cliccate qui. |
-
Prossimo Argomento: #M-13 Logaritmi – una breve introduzione
Indietro alla Lista Principale
Cronologia Glossario Matematica indice
Autore e Curatore: Dr. David P. Stern
Ci si può rivolgere al Dr. Stern per posta elettronica (in inglese, per favore!):
stargaze("chiocciola")phy6.org
Traduzione in lingua italiana di Pietro Sauro
Aggiornato al 25 Novembre 2001
 Esiste una semplice relazione tra queste due e quelle precedenti. Abbiamo
Esiste una semplice relazione tra queste due e quelle precedenti. Abbiamo