(5c) Coordenadas
Las Coordenadas son grupos de números que
describen una posición: posición a lo largo de
una línea, en una superficie o en el espacio. La latitud
y longitud o la declinación y ascensión recta, son
sistemas de coordenadas en la superficie de una
esfera: en el globo de la Tierra o en el globo de los
cielos. Coordenadas en el plano
El sistema más usado es de las coordenadas cartesianas, basado en un juego de ejes perpendiculares entre sí. Fue conocido con el nombre de René Descartes ("Dey-cart"), un científico y filósofo francés que, hacia el año 1600, ideó una forma sistemática de designar cada punto en el plano por medio de dos números. Puede que esto ya le sea familiar a usted. El sistema se basa en dos líneas rectas ("ejes"), perpendiculares entre sí, cada una marcada con las distancias desde el punto donde se juntan ("origen"): los espacios hacia la derecha del origen y hacia arriba de él, se toman como positivos y para los otros lados como negativos (vea el dibujo abajo).
Las gráficas usan ese sistema, al igual que algunos mapas.
Es simple y claro, una vez que se toma la decisión de en qué lado de la hoja es positiva z. Por común acuerdo, las ramas positivas de los ejes (x, y, z), siguen el pulgar y los dos primeros dedos de la mano derecha, en el mismo orden, cuando se extienden de tal forma que formen el mayor ángulo entre ellos. Lo que sigue usa las funciones trigonométricas seno y coseno. Si no está familiarizado con ellas, pase por alto esta sección o puede aprender sobre ellas. Coordenadas Polares
Las coordenadas cartesianas (x, y) no son la única forma de designar un punto P en el plano con un par de números. Existen otras formas y pueden ser más útiles en circunstancias especiales. Un sistema (llamado de "coordenadas polares") usa la longitud r de la línea OP desde el origen hasta P y el ángulo que forma esa línea con el eje x. Los ángulos se denominan, a menudo, con letras griegas y aquí seguimos las convenciones designándolo como f (f griega). Observe que mientras en el sistema cartesiano x e y tiene roles muy similares, aquí están divididos: r denota la distancia y f la dirección. Las dos representaciones están muy relacionadas. De las definiciones de seno y coseno: x = r cos f y = r sin f Esto permite que (x, y) se deduzcan de las coordenadas polares. Para ir en sentido inverso y deducir (r, f) de (x, y), observe que de las ecuaciones superiores o del teorema de Pitágoras se puede deducir r: r2 = x2 + y2 Una vez que se conoce r, el resto es fácil cos f = x/r sin f = y/r Estas relaciones solo fallan en el origen, donde x = y = r = 0. En ese punto, f está indefinido y se puede escoger para él lo que uno quiera. En el espacio tridimensional, la designación cartesiana (x, y, z) es exactamente simétrica, pero algunas veces es conveniente seguir el sistema de coordenadas polares y designar la distancia y la dirección por separado. La distancia es fácil: se toma la línea OP desde el origen hasta el punto y se mide su distancia r. también puede deducirse del teorema de Pitágoras, como en este caso: r2 = x2 + y2 + z2 Todos los puntos con el mismo valor de r forman una esfera de radio r alrededor del origen O. En una esfera se puede designar cada punto por la latitud l (lambda, l minúscula griega) y longitud f (phi, f minúscula griega), luego la posición de cualquier número en el espacio se define por 3 números (r, l, f). Azimut y Elevación
El teodolito está diseñado para medir esos ángulos. El ángulo f se mide en el plano horizontal, se le conoce como azimut y se mide desde la dirección norte. Una mesa giratoria permite al teodolito apuntar hacia cualquier azimut. El ángulo l se llama elevación y es el ángulo con el que el teodolito se eleva sobre la horizontal (si mira hacia abajo, l es negativo). Los dos ángulos juntos pueden, en principio, especificar cualquier dirección: f tiene un rango de 0 a 360º, y l de -90º (perpendicular hacia abajo o "nadir") a +90º (perpendicular hacia arriba o "zenit"). De nuevo se necesita decidir desde qué dirección se mide el azimut, esto es, ¿donde está el azimut cero? La rotación de los cielos (y el hecho de que la mayoría de la humanidad vive al norte del ecuador), sugiere (para mediciones topográficas) la dirección norte, y esta es de hecho la dirección que se toma habitualmente como el punto cero. El ángulo del azimut (visto desde el norte) se mide en sentido antihorario. Los matemáticos, no obstante, prefieren su propia notación y reemplazan "latitud" (o elevación) l, con colatitud q = 90 - l grados. No el ángulo con el horizonte, sino el ángulo con la vertical. El ángulo q (theta, una de las dos "tes" en griego) va de 0 a 180º, no de -90º a + 90º. Esto efectivamente puede tener más sentido, porque es más fácil medir un ángulo entre dos líneas (OP y la vertical) que entre la línea y el plano (OP y la horizontal).]
|
Página principal en Español (índice)Próxima etapa: #6 El Calendario Línea del tiempo Glosario (en Inglés) Author and Curator: Dr.
David P. Stern Last updated 12 September 2003 |


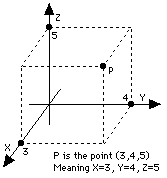 Funciona bien en una
hoja de papel plana, pero el mundo real es tridimensional
y a veces es necesario designar los puntos en dicho
espacio tridimensional. El sistema cartesiano (x, y)
puede extenderse hacia las tres dimensiones añadiendo
una tercera coordenada z. Si (x, y) es un punto en una
hoja, entonces el punto (x, y, z) en el espacio se
consigue situándose en (x, y) y elevándose una
distancia z sobre el papel (los puntos por debajo del
papel tienen z negativa).
Funciona bien en una
hoja de papel plana, pero el mundo real es tridimensional
y a veces es necesario designar los puntos en dicho
espacio tridimensional. El sistema cartesiano (x, y)
puede extenderse hacia las tres dimensiones añadiendo
una tercera coordenada z. Si (x, y) es un punto en una
hoja, entonces el punto (x, y, z) en el espacio se
consigue situándose en (x, y) y elevándose una
distancia z sobre el papel (los puntos por debajo del
papel tienen z negativa). 
