(11a) Las Elipses y la 1ª Ley de Kepler
Como se ha dicho anteriormente, existen otros caminos para fijar los
puntos en un plano. Por ejemplo, un punto P puede ser fijado mediante
su distancia r al punto central O ("origen") y el ángulo
φ (ó f griega), donde la línea
OP produce una dirección determinada. Tales "coordenadas
polares" (figura de la izquierda, abajo) son las mejores para describir
el movimiento planetario.
La Elipse en Coordenadas PolaresDe nuevo, si todos los valores de (r,φ) en la curva están relacionados mediante alguna ecuación, se puede escribir de forma simbólicar = r(φ) donde la función r(φ) se dice que es la ecuación de la línea en coordenadas polares. La función más simple es un número constante a obteniéndose la línea r = a 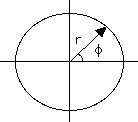
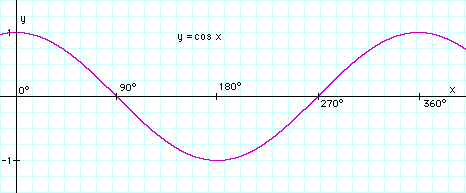
El valor de r es igual a a para cualquier valor de φ. Se obtiene el círculo alrededor del origen, con el radio igual a a, mostrado en el dibujo de la derecha. La ElipseConsidérese seguidamente la curva cuya ecuación esr = a(1- e2)/(1+ e cos φ) donde la excentricidad e es un número entre 0 y 1. Si e = 0 será, claramente, el círculo hallado anteriormente. ¿Y los otros valores? La función cos φ representa
un comportamiento como onda (dibujo inferior) y como φcos φ
= -1 . Aquí se muestra la tabla de los valores principales (360
está entre paréntesis, porque representa la misma dirección
que los 0 grados):
|
| φen grados |
|
90 | 180 | 270 | (360) |
| cos φ | |||||
| 1 + cos φ | 1 + e | 1 - e | 1 + e |
| Mientras e sea menor que1, el denominador será
siempre positivo. Nunca es cero, así que para cualquier φ que
se designe, se puede siempre encontrar una r
adecuada.
En otras palabras, la curva va por completo alrededor del origen, es cerrada.
La expresión (1 - e2) se puede separar en factores, o sea, se puede escribir como dos expresiones multiplicadas entre si ("el producto de dos expresiones"). Como se plantea en la sección sobre identidades algebraicas 1 - e2= (1 - e)(1 + e) En alguno de los puntos de la tabla inferior, una de las expresiones anula el denominador, dando: |
| φen grados | |||||
| r | a(1 - e) | a(1 - e2) | a(1 + e) | a(1 - e2) | a(1 - e) |
| La distancia de la línea desde el origen, de ese modo, fluctúa entre a(1-e) y a(1+e) y el resultado es un círculo achatado ó elipse; el punto O (el origen) es su foco. Todas las órbitas planetarias se asemejan a elipses, cada una con su propio valor de e ó excentricidad: la e menor corresponde a la forma más cercana al círculo. La órbita de la Tierra es muy cercana a la forma circular, con una e = 0.0168 y los otros planetas mayores (excepto Plutón) tienen excentricidades parecidas; si ve un dibujo a escala de esas órbitas en una hoja de papel, su vista no es capaz de distinguir que no es un círculo. La órbita del cometa Halley, por otro lado, tiene una e cercana a 1. |
|
Como se mencionó en la sección
precedente un segundo foco O' puede ser dibujado simétrico a
O, y la elipse puede definirse (su definición original, de hecho)como
la serie de puntos para los cuales la suma de R1+R2
de sus distancias a O y O' es siempre la misma.
La mayor dimensión de la elipse, su anchura AB a lo largo de la línea que conecta los dos focos, es su "eje mayor". Suponga que (R1,R2) son las distancias de A desde los focos O y O'. Entonces R1 = OA = a(1 - e) es la menor distancia de la elipse desde O, R2 = O'A = OB (por simetría) es la más larga y por lo tanto igual a (1 + e). Pero OA + OB = AB, así pues |
|
|
| Por ello la cifra a en la ecuación de la elipse
se conoce como eje semi-mayor. Ahora podemos establecer la
ley de Kepler de forma más precisa diciendo que "el cuadrado del
periodo orbital T es proporcional al cubo del eje semi-mayor
de su órbita alrededor del Sol."
Las dos cantidades (a,e) definen completamente la elipse.
Cuando esa elipse es la órbita de un planeta o satélite,
forman dos de los seis elementos orbitales que definen
la condición de cuerpo orbitante. Un tercer elemento, la anomalía
media, especifica la posición del planeta o satélite
a lo largo de la órbita y las tres restantes definen la orientación
de la órbita en el espacio tridimensional. Se puede encontrar más
sobre los elementos orbitales en la sección
(12a) Refinando la Primera LeyLa primera ley de Kepler es:"La órbita de un planeta es una elipse con el Sol en un foco" Normalmente, esto no es exacto al 100%. Imagine el planeta haciéndose más y más pesado de forma mágica, mientras que el Sol se hace más y más ligero. En algún punto ambos serán igual de pesados: ¿podemos decir cual orbita alrededor de cual? Para ser completamente exacta, la primera ley debería colocar el foco de la elipse orbital en el centro de gravedad del sistema Sol-planeta. (El centro de gravedad se definirá más tarde, pero por intuición, si las masas son muy desiguales, como entre un planeta y el Sol, se sitúa cerca del centro del objeto más pesado). Como el Sol es mucho más pesado que Marte, el efecto en la órbita de Marte (que estudió Kepler) es muy pequeña para que él lo notase. No obstante, el Sol también se mueve en respuesta a los movimientos de sus planetas y los movimientos de este tipo se han convertido en una herramienta importante en la búsqueda de planetas en el exterior del sistema solar. Un planeta del tamaño de la Tierra orbitando a una estrella distante estará lejos y oscuro par ser visto con cualquier telescopio terrestre, especialmente contra el resplandor de su sol, la misma estrella. Sin embargo, cuando el planeta va alrededor de su órbita, su estrella también se mueve en una órbita refleja exacta alrededor del centro de gravedad común. Es una órbita mucho menor y con un movimiento mucho más lento, porque el centro de gravedad está muy cercano al centro de dicha estrella (en el sistema Tierra-Sol, está dentro del Sol), pero puede ser detectado mediante las sutiles variaciones de la luz de la estrella. Recientemente se han encontrado algunos de dichos planetas, pero la mayoría son del tamaño de Jupiter y no parecen adecuados para la vida. La búsqueda, sin embargo, continúa y el descubrimiento más reciente (15 de Abril de 1999) ha sido el sistema de epsilon Andrómeda que aparenta contener como mínimo 3 planetas. Los cuerpos del sistema solar se pueden mover también en otras secciones cónicas, en parábolas ó hipérbolas, cuyas ecuaciones se asemejan a las de la elipse, pero tienen una e igual ó mayor que 1 . Estos cuerpos no están ligados al Sol y son libres de escapar de él. El denominador en la ecuación de la trayectoria r = a(1 - e2)/(1 + e cos φ) se hace cero para algunos valores de φ, haciendo r infinito y cuando el objeto móvil se acerca a esos valores se mueve más y más lejos, sin límite. Los cometas tienen, en general, una excentricidad e cercana a 1, sugiriendo que vienen de confines muy distantes del sistema solar. La sonda espacial Voyager 2 tiene una e > 1, está en camino fuera del sistema solar y nunca regresará. |
|
Próxima Etapa: #12 2ª Ley de Kepler
Author and Curator: Dr. David P. Stern
Last updated 13 December 2001
|