(M-10) La Trigonometría para ángulos mayores de 90°
| "Astrónomos" introdujo dos formas de describir la posición
de un punto P en un plano (p.e. una hoja de papel): las coordenadas cartesianas
(x,y) y las polares (r, φ).
Ambas usan como referencia un punto O ("origen") y un línea recta a través de él ("el eje x"). En las coordenadas cartesianas se dibuja un segundo "eje y" por O, perpendicular al primero, y se dibujan desde P unas líneas paralelas a los ejes, que cortan los ejes en los puntos A y B del dibujo. Las distancias OA y OB nos dan los números que definen P, las coordenadas x , y del punto. En coordenadas polares, el punto P se define por su distancia r desde el origen O (vea el dibujo) y su ángulo polar ("azimuth" en un mapa) entre el eje de las x y el "radio" r = OA, medido antidextrogiro (hacia la izquierda). Como la figura OAPB es un rectángulo, la distancia AP es igual a y. Por consiguiente sen φ = y/r
Multiplicando todo por r nos da la relación entre los dos sistemas de coordenadas (los símbolos que están juntos se están multiplicando): φ x = r cos φ
Estas relaciones permiten que puedan ser calculadas (x,y) cuando se proporciona (r, φ). Opuestamente, dados (x,y), lograr (r, φ), obsérvese que en el triángulo OAP, por Pitágoras x2 + y2 = r2 Por lo tanto, dados (x,y), se puede calcular r y luego (sen φ, cos φ) se pueden calcular como antes sen φ = y/r
(excepto en el punto de origen O, donde (x, y, r) son cero y las fracciones anteriores se hacen 0/0; se puede escoger cualquier valor para el ángulo φ). Sin embargo, continúa existiendo un problema. El ángulo φ tal y como se ha definido anteriormente puede ir desde 0 a 360°, pero (sen φ, cos φ) están definidos para 0 a 90°, cubriendo solo la parte del plano donde x e y son positivas. Cuando uno o ambos son negativos, el ángulo φ es mayor de 90 grados, y esos ángulos nunca aparecen en ningún triángulo rectángulo. ¿Qué solución (sen φ, cos φ) podemos tener para φmayor de 90 grados? Es simple: use las ecuaciones anteriores para redefinir el sen φy el cos φ para esos ángulos. Las ecuaciones son sen φ = y/r
Se ven ahora como nuevas definiciones del seno y del coseno, para el ángulo polar φformado por x e y. Si (x,y) son positivos, el resultado es exactamente el mismo que para los ángulos dentro de un triángulo rectángulo. Pero también es válido para ángulos mayores. Ahora el seno y el coseno pueden ser negativos (como x e y) pero su magnitud no puede exceder de 1, debido a que la magnitud de x e y nunca es mayor que r. He aquí los signos: |
| Rango | sen φ = y/r | cos φ = x/r |
|---|---|---|
| 0-90° | + | + |
| 90°- 180° | + | - |
| 180° - 270° | - | - |
| 270°-360° | - | + |
| Permitiendo ir a la línea OP alrededor del origen más
de una vez hace crecer al ángulo φmás
de 360°; el seno y el coseno se siguen definiendo como y/r e x/r, y
repite sus valores anteriores. Igualmente, girando OA en la dirección
opuesta,
a derechas, se definen valores negativos de φ.
Conjuntamente, esas extensiones definen los (sen φ,
cos φ) para cualquier ángulo φ,
positivo o negativo, de cualquier medida.
La relación derivada del teorema de Pitágoras sin2 φ+ cos2 φ = 1 sirve para cualquiera de esos ángulos. Si el seno o el coseno es cero, la otra función debe ser +1 ó -1, dependiendo del signo de la coordenada (x o y) que los definen. A 90° y 270°, x = 0 y por lo tanto cos φ = 0, mientras que a 0° y 180° y = 0 y por lo tanto sen φ = 0. Luego obtenemos |
| Ángulo | sen φ = y/r | cos φ = x/r |
|---|---|---|
| 0° | 0 | +1 |
| 90° | +1 | 0 |
| 180° | 0 | -1 |
| 270° | -1 | 0 |
| 360° | 0 | +1 |
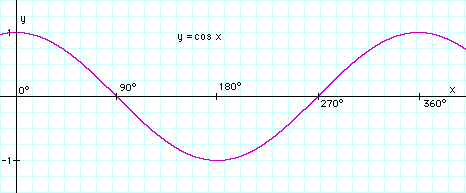
| Por supuesto, φ= 0° y φ
= 360° representan la misma posición de r, a saber, a lo largo
de la rama positiva del eje x . debajo está la gráfica del
cos φ:
|
Página principal en Español (índice)Índice Matemático Linea del Tiempo Glosario . Próxima Etapa (opcional): #M-11 Deducir el sen(a+b), cos(a+b)
Author and Curator: Dr. David P. Stern
Last updated 13 December 2001
|