(M-11a) Ejercicios de Trigonometría
| Las secciones (M 6-11) le proporcionaron algunos principios de trigonometría. Esta sección puede depararle la práctica aplicando dichos principios. En algunos casos se dan las soluciones, pero no las mire hasta que haga los esfuerzos necesarios para resolverlas usted mismo |
Hemos intentado evitar ejercicios repetitivos:
cada conjunto es diferente. Hágalos todos, ¡no deje ninguno!
Asumimos que dispone de una calculadora que puede deducir senos
y cosenos y que también dispone de las funciones sen-1
y cos-1 que sirven para encontrar el ángulo A a partir
del senA o el cosA, en la gama de 0 a 180 grados.
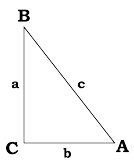 Un triángulo ABC tiene un ángulo recto C y dos ángulos
agudos A y B. Los lados del triángulo AC y BC de ambos lados del
ángulo recto C están dados como:
Un triángulo ABC tiene un ángulo recto C y dos ángulos
agudos A y B. Los lados del triángulo AC y BC de ambos lados del
ángulo recto C están dados como:
(b) AC = 5 BC = 12 (c) AC = 8 BC = 15
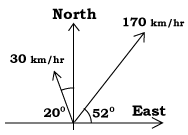
Indiquemos la velocidad del aeroplano relativa al aire como V, la velocidad del viento relativa a tierra como W, y la velocidad del aeroplano relativa a tierra U=V+W, donde la suma es uno de los vectores. Dibuje un diagrama con las velocidades dadas y con los ángulos adecuadamente designados. Para ejecutar la suma real cada vector debe descomponerse en sus componentes. Obtenemos Vx = 170 cos(52°) = 104.6 Vy = 170 sen(52°) = 133.96 Wx = -30 sen(20°) = -10.26 Wy = 30 cos(20°) = 28.19 Sumando: De Pitágoras, dado que U2 = Ux2 + Uy2, U= 187.63 km/h Por consiguiente
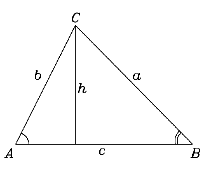
Pista: Desde C dibuje una línea CD perpendicular al lado c. La
línea CD es una "altura" del triángulo y por consiguiente
se podrá denominar por la letra h. Use h en su prueba.
|
Por consiguiente, la "ley de los senos" es completamente simétrica: senA/a = senB/b = senC/c
|
| El problema: En el triángulo ABC, la línea AB
está a lo largo de una ribera estrecha. Medimos la distancia c =
AB como 118 m, y los ángulos A y B tiene 63° y 55° . ¿Cuál
es la distancia b = AC?
No lea más hasta que intente resolverlo. Los
profesores, en clase, pueden sustituir las cifras y las direcciones.
|
| Debido a que la suma de todos los ángulos es de 180º, el
ángulo C debe ser igual a 62°. Luego por la ley de los senos
Multiplique ambos lados por el sen(55) para obtener la longitud b = AC. Pregunta adicional: ¿cual es la distancia perpendicular
desde C a la línea c = AB? (pista: es igual a la altura h en la
deducción del problema (4).)
|
El número n ("índice de refracción") es una propiedad del cristal y es mayor que 1. El problema: dando valores a A=0, 20, 40, 60, y 80 grados y n = 1.45, ¿cuál es el valor de B en cada caso? |
|
Si esta fórmula no funciona por cualquier motivo, el rayo no puede salir del cristal, sino que se refleja sobre la superficie límite de nuevo hacia el cristal como en un espejo ("reflexión interna total") El problemo: Dado B = 0, 20, 90, 60, 80 --¿cuáles son los ángulos A? ¿Con alguno de estos no sale el rayo del cristal ?
|
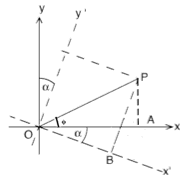
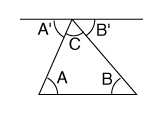
Usando los puntos auxiliares (C,D,E) y la líneas auxiliares AE ay AD, exprese x' e y' en términos de x, y, sena y cosa. Pista (siga estos pasos en el dibujo).
Los dos triángulos CBO y
CPA son rectángulos, y como la suma de los ángulos de un
triángulo es 180º, los dos ángulos agudos de cada uno
suman 90º. De estos ángulos agudos, los dos que se encuentran
en C son iguales y, por consiguiente, los otros dos también serán
iguales.
Recuerde: en un triángulo rectángulo con una ángulo a, si multiplica el lado largo
x' = OB = OD-BD = OD-AE = OA cosa - AP sena = x cosa - y sena y' =BP = BE+EP = AD+EP = OA sena + AP cosa = x sena + y cosa Escribamos el resultado final: x' = x cosa - y sena y' = x sena + y cosa Práctica de Álgebra: usando las dos relaciones
anteriores, ¿puede expresar (x,y) en función de (x',y')?
Deberá usar sen2a + cos2a= 1.
Eso también estará de acuerdo con la figura, en
donde (x,y) se obtiene girando (x',y') a izquierdas un ángulo a,
que puede ser visto como una rotación a derechas un ángulo
(-a).
¿También es válida la fórmula para latitudes sur? (b) ¿Es esta la única solución? Pistas: (a) Use cos2X = 4 sen2X (b) Dado que trabajamos con una ecuación que solo implica cuadrados, cualquier solución de ella solo impone sen2X y cos2X. Sin embargo, la condición original también requiere que cos X y sen X tengan el mismo signo algebraico. |
Página principal en Español (índice)Índice Matemático Linea del Tiempo Glosario .
Author and Curator: Dr. David P. Stern
Last updated 13 December 2001
|