• La tangente es una herramienta de trigonometría relacionada con el seno y el coseno. En este sitio web es usada en relación a la alidada.

  Usted ya sabrá que los triángulos rectángulos son básicos en Trigonometría. Sea ABC un triángulo (dibujado) con C = 90° el ángulo recto y A, B los ángulos agudos. Sean también a, b y c las longitudes de sus tres lados: a del lado opuesto a A, b del lado opuesto a B, y c, el más largo, opuesto a C.

  Dos razones útiles asociadas con el ángulo A ("funciones trigonométricas de A") son:

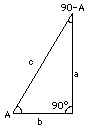
El seno de A,    sen A= a/c         (implicando al lado a opuesto a A)

El coseno de A, cosA = b/c                (implicando al lado b contiguo a A)

Estas dos razones implican al lado largo c ("hipotenusa", en lenguaje matemático), y por cuanto a y b deben ser más pequeños que ese lado, estas razones son siempre números menores que 1. Ahora añadiremos dos razones más a nuestra colección: la tangente y la cotangente:

La tangente de A, tan A = a/b                 (a veces escrita "tg A") .
Y la cotangente de A, cotan A = b/a = 1/tan A                            

Existe una simple relación entre ese par de razones primeras. Tenemos:

senA / cosA= (a/c) / (b/c)

Multiplicando arriba y abajo por c (es lo mismo que multiplicar la fracción por (c/c)=1) se obtiene:

senA / cosA = (a/b) = tan A

Invirtiendo la fracción:

cosA/ senA = 1/tanA = cotanA

Las calculadoras que ofrecen senos y cosenos, y los libros que tabulan sus valores, son capaces también de ofrecer tangentes y cotangentes.

Una simple aplicación

A mediodía, un mástil vertical de 15 m (50 pies) de altura tiene una sombra de 5,4 m (18 pies) de longitud.. ¿Cuál es el ángulo A del sol sobre el horizonte? (Como se explica en la sección "Navegación", ese ángulo le permite a uno calcular la latitud de su posición). Del esquema dibujado:

tanA = 15/5,4 = 2,7778

Si usted dispone de una tabla de tangentes, puede ahora buscar dos ángulos cuyas tangentes sean valores que estén uno inmediatamente por encima de ese valor y el otro por debajo de ese valor, y estimar así dónde se encuentra A entre ellos ("interpolación"). Las calculadoras normalmente tienen un botón "tan" que, si se introduce previamente el ángulo, nos da el valor de la tangente. Pero muchas también tienen un botón "tan ^-1 " que hace la inversa: dada la tangente, devuelve el ángulo. (Podría ser el mismo botón, calculándose tan^-1 si primero se pulsó un botón de "modo especial" (a veces de color); tan^-1 se llama también "la tangente inversa" o "el arco tangente"). En este ejemplo:

tan^-1 2,7778 = 70,2°

P.S.: Una tangente a un círculo es una línea que lo roza en sólo un punto. Si alguna vez se ha preguntado cómo entró la palabra "tangente" a la Trigonometría, haga clic aquí.