Note: Dans cette section, les quantités vectorielles sont indiquées en gras

Vous êtes dans un bateau, et vous naviguez à une vitesse u un jour sans vent. Un petit drapeau est attaché au mât: dans quelle direction se dirige -il ?

    Mais si ce n'est pas un jour sans vent ? Si le vent souffle à une vitesse v ? Vis à vis du bateau, l'air se déplace maintenant à une vitesse v - u , une somme de vecteurs, combinaison de v et de la direction du bateau ("dans la référence du bateau"). Le drapeau ne se dirige plus maintenant tout à fait vers l'arrière mais dans une orientation intermédiaire.

    Et maintenant, si le bateau change de direction : Par rapport à lui u se dirige encore vers l'arrière, mais le vent semble maintenant venir d'une autre direction, toujours par rapport au bateau. En conséquence, et suivant la combinaison de la direction de v et de celle du drapeau, la résultante prends une nouvelle orientation, v - u,

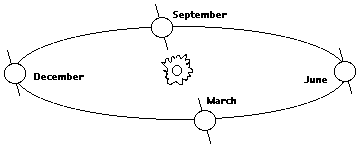
Le déplacement apparent des étoiles

    Comme déjà vu dans la section sur la parallaxe, cela pourrait suggérer que la distance de l'étoile polaire soit de 1/40 de parsec , moins de 0.1 année - lumière. Cependant, les décalages de position ne survienne pas à l'époque ou ils le devrait. Le décalage maximum de l'étoile polaire, observé depuis n'importe quel point, ne se produit pas quand la terre est située aux extrémités opposées de l'axe de son orbite, comme cela devrait être, mais 3 mois plus tard.

    Par exemple,dans le schéma ci-dessus, la différence de position apparente de l'étoile polaire devrait être la plus importante entre la direction "décembre" de la terre et la direction "juin", dans la mesure où elle ci est observée depuis les extrémités du grand axe. En réalité, cela se produit en septembre, quand la terre s'est déplacée de 90° par rapport à sa position de juin. Ce qui compte finalement, n'est pas le déplacement de la terre, mais sa vitesse, qui en septembre la place dans la direction du déplacement de l'étoile polaire.

Explication de Bradley

    Depuis les travaux de Ole Romer, un Danois travaillant à l'observatoire de Paris sur les éclipses d'un satellite de Jupiter, en 1675,on connaissait la vitesse de la lumière, aujourd'hui universellement notée par la lettre c (comme dans "E=mc²"-- La vitesse u de la terre sur son orbite était aussi approximativement connue. Dans le cadre de référence de la terre, mobile, le reste de l'univers présente une vitesse -u, perpendiculaire à la vitesse c de la lumière émise par l'étoile polaire. Combinez vectoriellement les deux, et vous obtenez le déplacement observé.

    [ On pourrait se demander : quand faut-il utiliser u et quand doit-on utiliser (-u)?
    Si on est à l'extérieur et que l on observe un objet se déplacer avec une vitesse u, par exemple, un avion soumis à un vent latéral, on ajoute u aux autres mouvements.
    mais si u est la vitesse à laquelle nous, les observateurs, sommes en mouvement, l extérieur se déplace par rapport à nous avec une vitesse (-u). Dès lors (-u) doit alors être ajouté à n'importe quel autre mouvement observé dans le monde extérieur.]

    Aujourd'hui, nous sommes savons bien qu'ajouter -u à la vitesse de la lumière des étoiles est en principe incorrect : si des vitesses proches de c sont en jeu, les formules de la relativité d'Einstein, doivent être employées. En ajoutant -u à c de façon classique, on obtient une vitesse supérieure à c, alors que la théorie de la relativité dit que la vitesse de la lumière est toujours égale à c, indépendamment de la façon dont on l'observe. Cependant, il s'avère que le déplacement calculé par Bradley sur la direction est identique à ce que donnerait la relativité. Calculons- la à la manière de Bradley, en ignorant la relativité et en utilisant la même "pré trigonométrie" présentée dans la section sur la parallaxe.

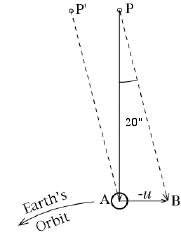
    Dans le schéma, A est la terre , AP la direction de l'étoile polaire (l'étoile elle-même est beaucoup plus éloignée). Le vecteur PA représente la vitesse de la lumière en provenance de l'étoile polaire à c =300,000 km/s. Le vecteur AB représente la vitesse -u de la terre par rapport à l'étoile polaire, égale en grandeur à la vitesse de la terre sur son orbite u= 30 km/s, mais en direction opposée. (pour simplifier le calcul admettons que AP soit perpendiculaire à AB,(dans ce cas le mouvement apparent de l'étoile est un cercle ; en réalité l'angle, habituellement plus petit que 90°, confère au mouvement apparent la forme d'une ellipse et non celle d' un cercle.) Le point P' indique la direction apparente de l'étoile polaire, vue de la terre, déviée d'un angle a α° = 40" de sa direction réelle.

    Chaque degré contient 60 minutes d'arc (60 ') et chaque minute contient 60 secondes d'arc (60"), (unités indépendantes des minutes et secondes de temps). Chaque degré égale donc 3600", et donc :

    Une demie année après la direction de u est inversée et le déplacement se trouve en direction opposée, donnant une amplitude annuelle d'environ 40", comme il avait été observé.

Aberration du vent solaire

Si b est l'angle de déviation du vent solaire vu de la terre, alors :

    Pour un vaisseau spatial destiné à explorer la queue, dirigée " du côté nuit ", comme le japonais "Geotail" (à une distance d'environ 200 rayons terrestre), cet effet doit être pris en considération pour le placer dans la queue et non pas à côté. Malheureusement, la direction de v change également inopinément de quelques degrés, de sorte que, bien que b soit pris en considération, le calcul de la position centrée sur l'intérieur de la queue, est souvent erroné.

    Une aberration beaucoup plus grande est prévue pour la sonde spatiale solaire, le projet de la NASA pour l'observation du vent solaire à proximité du soleil. Son orbite la fera s'en approcher de moins de 4 rayons solaires, où elle évitera la fusion, due à l'intense chaleur, en étant protégée par un bouclier thermique spécialement conçu.

    Une fois enfermé dans ce bouclier excluant la lumière du soleil, on peut se demander comment observer le vent solaire, qui, comme la lumière, s'écoule radialement à l'extérieur ? Grâce à l'aberration, la sonde solaire se déplacera au plus proche, (au périhélie) à environ 300 km/s, de sorte que le vent solaire , circulant à 400 km/s (pas comme la lumière ! ) sera dévié d'environ 37°, lui permettant d'atteindre les détecteurs placés derrière le bouclier thermique.

Post-scriptum : Données sur l'espace
obtenues grâce au Laser

    On a proposé une solution, utilisant un laser depuis la terre. Au lieu d'un émetteur radio, le satellite porterait un prisme réflecteur réfléchissant directement le faisceau vers son point de départ ; On avait d'ailleurs essayé avec un réflecteur laser mis en place sur la lune par les astronautes et un télescope terrestre puissant pour détecter le faisceau renvoyé. Dans un satellite, un dispositif électronique de très petite puissance modulerait le rayon laser, en fonction des données à transmettre. Puisque le retour du rayon laser reprend le même chemin, la station de détection pourrait être placée juste à côté du laser émetteur.

    Assez astucieux, n'est ce pas ? Oui mais seulement jusqu'à ce que les promoteurs se soient rendus compte que l'aberration (du type de celle de Bradley ) décalerait le faisceau renvoyé, en raison du déplacement rapide du satellite (à la différence de la lune). Le décalage peut atteindre des dizaines ou des centaines de mètres, en directions variables selon le mouvement du satellite. Pour cette raison , l'idée a été abandonnée.