(11) Graphiques et Ellipses
|
Les lois du mouvement orbital sont mathématiques, et on ne peut pas les apprendre sans quelques mathématiques. Les maths utilisées ici sont plutôt élémentaires; (si vous avez besoin d'un rappel, cliquez ici.) Autrement, vous pouvez sauter juste les équations et suivre le récit. Description mathématique d'une courbeComme déjà dit, le système cartésien repère n'importe quel point d'un plan (par exemple une feuille de papier plate) par sa distance, évaluée par un couple de deux nombres (x,y), à deux axes perpendiculaires. Ces nombres sont connus comme "coordonnées" du point. |
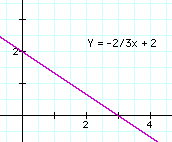
Dans un plan, une ligne, droite ou courbe, est constituée de beaucoup de points, chacun ayant ses propres coordonnées (x,y). Souvent, il existe une formule ("équation") qui relie x à y : par exemple, les lignes droites ont une expression: y = ax + b dans laquelle toutes les paires de nombres (a , b), positif, négatif ou zéro, composent une certaine ligne droite. La représentation sur un plan de droites obtenues par ce genre d'expression, (venant de n'importe quelle source, même d'observation pure, par exemple la température suivant le temps) est dénommée "graphique". y = a x2 |
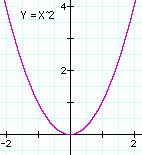
donne une parabole, pour toute valeur de a . Habituellement (cependant pas toujours) on isole y, de sorte que la formule prend la forme y = f(x) ou f(x) signifie "n'importe quelle expression impliquant x", ce qui se dit en termes mathématiques, "fonction de x." Les courbes dessinées ici en exemple sont,
et pour la parabole y = x2. Droite: |
| x | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 8/3 | 2 | 4/3 | 2/3 | 0 | -2/3 |
Parabole:
| x | -2 | -1.5 | -1 | -0.5 | 0 | 0.5 | 1 | 1.5 | 2 |
| y | 4 | 2.25 | 1 | 0.25 | 0 | 0.25 | 1 | 2.25 | 4 |
L'équation du cercleLa grande majorité des graphiques sont donc issus de formules, données sous la forme =
Une telle forme permet de trouver très facilement les points du graphique puisqu'il n'y a qu'à choisir x et calculer f(x) (= une certaine expression donnée impliquant x)pour obtenir la valeur correspondante de y. N'importe quelle équation impliquant x et y peut être utilisée comme une application à un point du graphique. La principale difficulté est qu'avec des équations plus compliquées, quand x est choisi, trouver y, qui lui correspond, exige un supplément de travail, (et parfois il est plus facile de choisir y et de trouver x). Le graphique le plus connu de ce genre est sans doute le cercle, de rayon R, dont l'équation
Tracez un cercle de rayon R ,centré en O sur un système d'axes (x,y). De n'importe quel point P de ce cercle, tracé selon les valeurs indiquées de (x,y), menez une perpendiculaire à l'axe des abscisses: elle tombe au point A |
|
|
|
Ici x et/ou y peuvent être négatifs, s'ils sont à gauche de l'axe des ordonnées, ou sous l'axe des abscisses, mais indépendamment de leur signe, x2 et y2 sont toujours positifs. Puisque le triangle OAP est droit, le théorème de Pythagore, s'applique, et pour n'importe quel point P, on a toujours la relation:
Que l'on peut également écrire: L'équation du cercle est satisfaite pour n'importe lequel de ses points. Par exemple, si le graphique est défini par l'équation:
cette équation est satisfaite par tous les points énumérés ci-dessous: |
| x | 5 | 4 | 3 | 0 | -3 | -4 | -5 | -4 | -3 | 0 | 3 | 4 | ( 5 ) |
| y | 0 | 3 | 4 | 5 | 4 | 3 | 0 | -3 | -4 | -5 | -4 | -3 | ( 0 ) |
L'équation d'une ellipseL'équation du cercle reste toujours valable si on la divise des deux côtés par R2:
L'équation d'une ellipse en est une petite modification :
ou a et b sont deux nombres donnés. Par exemple, avec (8.4), à quoi le graphique ressemble- il ? Près de l'axe de x, y est très petit et l'équation devient proche de
et donc:
A cet endroit, le graphique ressemble donc à une partie de cercle du rayon a, dont l'équation serait
Exactement de la même manière on peut prouver que près de l'axe des ordonnées, où x est petit, y = ±b et la forme ressemble à cet endroit à un cercle du rayon b.
Exemple:Traçons l'ellipse
Nous savons tout de suite qu'elle coupe les axes àx=±8 et ày=±4. Maintenant, ajoutons quelques points:
|
|
(1) Prenons y = 2 .
| Enlevons 1/4 de chaque côté:
En prenant les racines carrées (ici la lettre √) et en ne calculant qu'avec 3/4: ( Finalement: x = 6.93 , avec une précision raisonnable. (2) Prenons y = 3 .
Soustrayons 9/16 des deux côté
Prenons la racine carrée ( avec 3 à 4 décimales ):
ce qui donne approximativement, x et y peuvent être positifs ou négatifs. Nous avons donc obtenu 12 points, suffisamment pour dessiner un graphique simplifié: |
| x | 8 | 6.93 | 5.29 | 0 | -5.29 | -6.93 | -8 | --6.93 | -5.29 | 0 | 5.29 | 6.93 | ( 8 ) |
| y | 0 | 2 | 3 | 4 | 3 | 3 | 0 | -2 | -3 | -4 | -3 | -2 | ( 0 ) |
C'est une prolongation normale de la définition du cercle, qui est la collection de tous les points à la même distance (le rayon R) d'un point donné (le centre). Un point définit un cercle, deux définissent une ellipse.
Les foyers sont toujours situés sur le plus long des deux axes, "le Grand Axe", du système (x,y) de l'expression ci dessus. Si a est plus grand que b, le grand axe se trouve sur l'axe des abscisses, et nous vous laissons le soin de démontrer que:
[Conseil : Faites un croquis de l'ellipse et des axes qui la définissent, marquez le point ou R1 et R2 croisent l'axe des abscisses, et examinez les]. La valeur de a dans une orbite elliptique, connue comme demi grand axe en astronomie, est considérée comme un des six éléments orbitaux qui définissent le mouvement selon les lois de Kepler.
Les foyers d'une ellipse ont une propriété intéressante. Un ellipsoïde de révolution est la figure à trois dimensions obtenue en tournant une ellipse autour de l'un de ses axes. Si un tel ellipsoïde est construit creux, et sa surface intérieure argentée pour agir en tant que miroir, alors si une source de lumière est placée à un des foyers, tous ses rayons convergeront vers l'autre. Même si seulement une partie de l'ellipsoïde est argentée, tout la lumière frappant cette partie sera encore concentrée sur l'autre foyer.
Les ondes sonores peuvent se comporter aussi comme la lumière. La salle du Capitole à Washington (USA), ou la chambre des représentants se réunissait, possède un plafond en quart d'ellipsoïde (moitié d'une moitié), avec ses foyers près du sol. Cette conception architecturale, datant de presque 200 ans, permet à une personne placée à l'un des foyers de bien entendre ce qui est dit à l'autre foyer, même des chuchotements. Assurément le concepteur, Daniel Webster a bien accompli sa tache et bien utilisé ce "truc" de la nature.
Aujourd'hui, les représentants à la chambre sont beaucoup plus nombreux, et on utilise une salle beaucoup plus grande. Cet ancien lieu de réunion est devenu une exposition de statues d'Américains célèbres.
Chaque année, des milliers de visiteurs sont conduits dans ce batiment. Au cours de leur visite, ils se regroupent près d'un foyer (identifié par un repère en laiton sur le plancher), pour écouter les murmures de leur guide, positionné à l'autre foyer. Par ailleurs, Samuel Morse, l'artiste qui a également inventé le télégraphe électrique, a réalisé un tableau de cette salle avec les portraits clairement identifiables de ses occupants . Une copie de cette peinture bien connue et son histoire y sont également exposées. L'original se trouve dans la galerie Corcoran, à Washington.
Prochaine étape: #11a Ellipses et première Loi de Kepler
Auteur et responsable : Dr. David P.
Stern
Dernière mise à jour : 12.23.2003
Un autre aspect de l'Ellipse

L' ensemble des points pour qui R1 + R2
ont la même valeur est une ellipse
L'ellipse était déjà bien connue des scientifiques de la Grèce antique (connus comme "philosophes", amoureux de la sagesse), mais ils l'ont définie différemment. Pour eux l'ellipse était l'ensemble des points (dans un plan) pour lesquels la somme des distances R1 + R2 ,tracés à partir de deux points, était la même (voyez le dessin).
Les deux points sont appelés foyers de l'ellipse (chacun est un "foyer"), et c' est important, puisque Kepler a constaté que le soleil occupe toujours un des foyers de l'ellipse que constitue l'orbite et non pas (comme on pourrait peut-être le penser) le "centre" d'origine de l'ellipse quand elle est exprimée par une équation dans un système d'axes (x,y), perpendiculaires. : Chuchotements au Capitole (USA)
Mail au Dr.Stern: stargaze("at" symbol)phy6.org
Traduction française: Guy Batteur guybatteur(arobase)wanadoo.fr
