(17b) Mesurer les masses par comparaison,
sans utilisation de la pesanteur
| Avec le plus simple des équipements, vous aussi pouvez effectuer des mesures de masse semblables à celles effectuées à bord de Skylab |
Il faut :
|
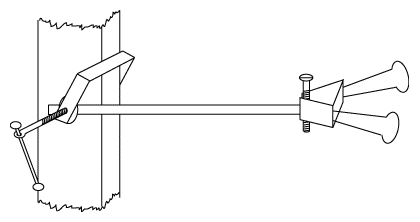 |
|
|
Instructions
|
| La théorie prévoit que la période d'oscillation est proportionnelle à la racine carrée de la masse oscillante, y compris celle de la pince. Notez que la pesanteur ne joue aucun rôle ici : la période d'oscillation serait la même sur la lune ou si g= zéro
La racine carrée étant écrite "SQRT", nous avons |
| ("le rapport de racines carrées est la racine carrée du rapport"). Multiplier chaque côté par lui-même :
(T2/T1)2 = (m2+m0)/(m1+m0). Si nous étions dans l'espace, nous mesurions T1 et T2, et connaîtrions les masses m1 et m0alors nous pourrions en déduire la valeur d'une masse inconnue m2. |
Résultat d'une expérience réelle :
| Poids : m1 = 50 gr, m2 = 120 gr,
m0 = 10 gr.
Le nombre d'oscillations, en 10 secondes, est de 20 pour m1, et pour m2, 13.5 oscillations. Donc : |
| T1 = 10 sec/20 = 0.5 sec
T2 = 10 sec/13.5 = 0.74074
sec.
De sorte que (T2/T1)2 =
2.195 il devrait égaler en théorie :
(m2+m0)/(m1+m0) =
130/60 = 2.167 |
| Ce résultat est probablement excellent pour une expérience aussi simple, en sachant que la masse de la lame de scie a été ignorée. |
Revenir à la liste principale
Mail au Dr.Stern: stargaze("at" symbol)phy6.org
.
