(24) Références des objets en rotations dans l'espace et sur terre
"Apesanteur"Soit un astronaute se déplaçant (approximativement) sur un grand cercle entourant la terre, en orbite basse terrestre. L'accélération exigée pour ce mouvement est fournie par la gravitation mg(RE/r)2= mv2/r mg est le poids de l'astronaute à la surface de la terre, où r = RE dans le terme de gauche. C'est naturellement la même équation que celle déjà utilisée pour démontrer l'étude de Newton sur la pesanteur. Mais on peut également l'écrire : mg (r/RE)2 - mv2/r = 0 Cela veut dire que par rapport à l'astronaute, il y a deux forces, la pesanteur et la force centrifuge, qui s'équilibrent complètement, leur somme étant égale à zéro. On dit parfois que les astronautes dans l'espace sont en "apesanteur". En réalité, ils restent toujours sous l'influence de la pesanteur terrestre. Il est vrai que l'astronaute n'a aucune tendance à tomber vers la terre, mais la vraie raison peut être énoncée de deux façons :
Simulation de " g zéro" dans un avionY a il un problème si l'orbite du vaisseau spatial n'est pas circulaire mais elliptique ? Cela ne fait aucune différence. Si la force de la pesanteur à la distance r est
On peut dire que l'équation du mouvement d'un objet uniquement soumi à F est
L'accélération a est celle du vaisseau spatial en orbite, vue du cadre fixe de la terre. Dans une orbite circulaire de rayon r, elle égale v2/r, alors que dans une orbite elliptique sa grandeur et sa direction sont différentes, mais peuvent également être calculées. La chose importante à noter ici est que l'astronaute à l'intérieur du vaisseau spatial est sujet à la même pesanteur et subit donc la même accélération que le vaisseau spatial lui-même. Dans le cadre du mouvement du vaisseau spatial , l'astronaute n'est pas attiré vers le plancher de la carlingue ni dans aucune autre direction, et a donc l'impression que la pesanteur est éliminée. Si, nouvelle situation, l'astronaute est placé dans une carlingue qui tombe en chute libre, assez près de la surface de la terre. Ici encore :
mais puisque r est très proche de RE, , ce rapport vaut 1, et on obtient simplement
La carlingue tombe avec une accélération g, et le passager tombe également avec la même accélération, si bien qu'ici encore, aucune force ne pousse le passager vers le plancher de la carlingue. Se référant à la carlingue environnante, le passager aura encore l'illusion que la pesanteur n'existe pas. C' est la même chose si la carlingue présente une vitesse constante préalable, par exemple si elle a été lancée avec une vitesse verticale initiale u et une vitesse horizontale initiale w parce que ni l'une ni l'autre de ces vitesses ci n'affecte les forces et les accélérations. La carlingue et le passager accélérèrent toujours vers le bas, avec a =g, créant l'illusion d'une pesanteur nulle. Si cette expérience était réellement entreprise, cette illusion, (et également la carlingue !) serait vite brisée par le contact brutal avec la terre. En outre, la résistance de l'air réduirait bientôt l'accélération de la carlingue au-dessous de g. Le passager à l'intérieur, toujours sujet à a = g, rattraperait alors la carlingue, un processus qui apparaîtrait dans ce cadre de la carlingue comme un retour partiel de la pesanteur. Cependant, on peut pratiquer sans risque la même expérience à bord d'un avion à haute altitude, capable de vaincre toute résistance de l'air par la poussée de ses moteurs. En prévoyant un chemin parabolique, semblable à celui d'un projectile soumis à la seule pesanteur, ce type d'avion peut créer à l'intérieur de sa carlingue un environnement d'apesanteur, pendant un temps limité. La NASA l'a fait avec KC-135, un avion à 4 moteurs à réaction, surnommé "la comète des vomissements" parce que son brusque passage à zéro g rend certains passagers tout à fait nauséeux . La carlingue de l'avion peut être mise transitoirement à zéro g. Elle est utilisée à la formation des astronautes ,et pour de courtes expériences sur des phénomènes à zéro pesanteur. La cabine est complètement isolée, et l'illusion "de pesanteur nulle" peut être maintenue pendant environ 20-30 secondes. Pour des images et des détails, cliquez lci.
En 2001, le film de science-fiction ": l'odyssée de l'espace " montrait une station spatiale en rotation. Cette rotation procurait à l'équipage" une pesanteur artificielle." C'était une structure en forme de roue, avec des tubes comme des rayons vers une carlingue centrale (dessin). Cette carlingue étant destinée aux transferts lors des visites d'autres vaisseaux spatiaux. Cliquer ici pour plus sur cette conception . En raison de la rotation, il y aurait effectivement une espèce de pesanteur, avec "le bas" vers l'extérieur (Larry Niven a développé cette notion dans un roman fantaisiste de science-fiction "Ringworld" et ses suites). Pour la calculer, le plus simple est d'employer la référence de la station et d'ajouter la force centrifuge à toutes les autres forces. Cependant, quand on se déplace dans cet espace en rotation, particulièrement pour parcourir les tubes, une force nouvelle s'ajoute, appelée " force de Coriolis ", du français Gaspard Gustave de Coriolis (1792-1843). 
Sur le schéma, un astronaute se déplace dans un des tubes , partant du point A pour se diriger vers B, utilisant très probablement une échelle, puisque ce mouvement s'oppose à la pesanteur artificielle de la station. Dans un cadre extérieur, " A " est un point quelconque ; L'astronaute tourne également autour de l'axe de la station. Aux points A et B, la vitesse de rotation s'exerce dans la même direction, mais est plus lente en B, parce que, plus proche de l'axe de rotation, elle concerne un plus petit cercle. En B, que devient alors la vitesse supplémentaire qu'avait l'astronaute en A ? Approximativement, d'après la première loi de Newton, l'astronaute tendrait à garder cette vitesse supplémentaire et serait donc constamment rejeté vers le côté du tube (Dans la direction des flèches). Cette poussée est dénommée " force de Coriolis ". Si le mouvement s'effectue en direction opposée, de B vers A, la direction de la force est elle la même ou renversée ? Trouvez le vous-même ! Les tourbillons dans une vidange de lavaboOn dit de temps en temps que l'eau s'écoulant dans la salle de bains tourbillonne dans des directions opposées selon que l'on se trouve au nord ou au sud de l'équateur. Le principe physique est correct, mais l'effet réel est si minime qu'il ne peut être observable lors des vidanges des lavabos de salle de bains. Mais le même effet est très important dans les tourbillons atmosphériques à grande échelle, tels les ouragans et les cyclones, et même pour la météo de tous les jours.. |
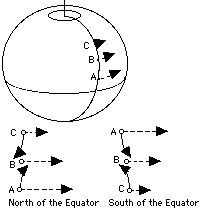
La terre, vue de dessus du pôle nord, tourne dans le sens contraire des aiguilles d'une montre. Imaginez 3 points de l'hémisphère nord , de même longitude géographique, A est (sur le dessin) le plus proche de l'équateur, B est légèrement plus loin et C encore plus loin. Chacun de ces points accompli un cercle complet autour de l'axe de la terre en une journée: A décrit le plus grand cercle, donc la plus grande distance et le déplacement le plus rapide, B, sur un plus petit cercle, se déplace plus lentement, et C encore moins vite. Ces points sont redéssinés à côté à plus grande échelle, avec des flèches en tirets indiquant direction et vitesse à la surface de la terre pour chaque point. Considérons maintenant l'air au-dessus de ces points. Si aucun vent ne souffle, l'air se déplace comme la surface. Sa vitesse, vue de l'extérieur ("vue de l'univers") est indiqué par les flèches - tirets, mais par rapport à la surface , elle reste partout égale à zéro. Par rapport à la terre en rotation, l'air reste aux points (A, B, C) et ne les quitte pas. |
|
Prochaine étape: A vous de choisir ! #25 Le Principe de la Fusée continue l'histoire des vols spatiaux. Revenir à la liste principale
Mail au Dr.Stern: stargaze("at" symbol)phy6.org
|


