(35) Vaisseaux vers les planètes et les étoiles
Collisions ElastiquesAu cours d'une partie de ping-pong, imaginons que les mouvements des raquettes, mobilisées à 20 milles par heure, poussent la balle -à 20 M/H, en direction opposée. A quelle vitesse la balle rebondit-elle ?(remplacez 20 M/H par 10 m/sec, si vous préférez employer les unités métriques.)
|

Généralement ce genre de problème exige l'utilisation des vecteurs, puisque la balle et les raquettes forment un angle. Les collisions frontales sont plus simples, puisque que les vitesses peuvent alors être considérées comme positives dans une direction et négatives dans l'autre. Nous pouvons alors imaginer une balle se déplaçant à -20 M/H et rencontrant une raquette se déplaçant à +20 M/H (figure supérieure ; le rebond est dessiné avec un angle mais est en réalité en direction opposée). Quelle est la suite ? Dans les problèmes sur les forces, ajouter la même vitesse à l'ensemble des mouvements ne change pas la physique. A l'intérieur d'un avion de ligne à réaction se déplaçant à 600 M/H les objets tonbent directement vers le bas, exactement comme ils le font à l'intérieur d'une maison. Ceci parce que, même en ajoutant 600 M/H, les accélérations (modifications de vitesse) ne changent pas, et qu'il n'y a qu'elles qui comptent dans les lois de Newton. Nous pouvons donc ajouter -20 M/H à toutes les vitesses. Dans ce cas, la vitesse de la raquette est maintenant nulle ( zéro) - ce qui signifie que nous sommes dans son "cadre de référence" -- tandis que la balle se déplace maintenant à (-20) - 20 = -40 M/H (schéma du centre). Nouvel aspect du problème : une balle se déplaçant à -40 M/H frappe une surface immobile ; si la collision est élastique (aucune énergie perdue), le retour de cette balle se fait à la même vitesse mais en direction opposée, c.-à-d. avec le signe de sa vitesse renversé. La vitesse de retour est donc +40 M/H. Et si, en plus, nous retournons au monde réel, en ajoutant +20 M/H à toutes les vitesses ? La raquette est de nouveau à 0 + (20) = 20 M/H, sa vitesse initiale, mais la balle passe à 40 + 20 = 60 M/H. Se heurter à la raquette en mouvement augmente la vitesse v de deux fois la vitesse de la raquette. Puisque l'énergie cinétique est proportionnelle à v2, tripler la vitesse de 20 à 60 M/H signifie que l'énergie a augmenté 9-fois ! L'énergie supplémentaire n'a été assurée que par la raquette et par la main qui la tient. |
|
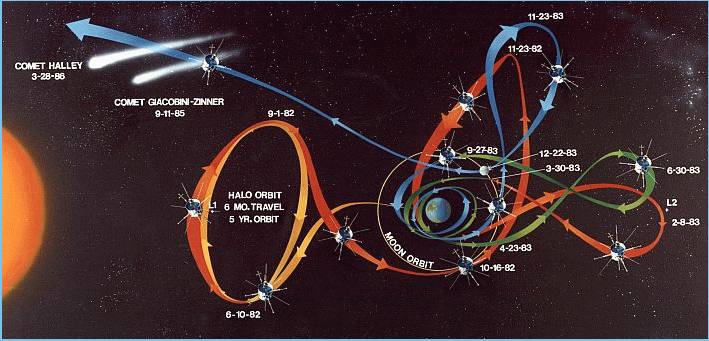
Ce type de manœuvre est souvent employée pour les sondes interplanétaires. La " rencontre " avec la lune a été également employée pour envoyer le vaisseau spatial vers le point L1 de Lagrange, ou le point L2 de l'autre coté, avec des missions nescéssitant des modifications (de type Geotail) ou le 22 décembre 1983 pour envoyer ISEE-3 loin de la terre vers la comète Giacobini-Zinner. (la figure ci-dessus décrit son orbite, qui inclut plusieurs rencontres avec la lune, les dates sont données). Le croisement avec la terre elle-même a été utilisé de cette façon, par la sonde spatiale Galiléo, satellisant actuellement Jupiter : la sonde a d'abord rencontré Venus, puis est revenue une première fois tourner autour de la Terre. Tout ceci ressemble à un billard cosmique, sauf que la "boule en mouvement," (le satellite faisant la rencontre), possède son propre petit moteur de fusée, pour corriger son cours si nécessaire et autoriser des trajectoires complexes. Cette manœuvre a été utilisée pour la première avec Mariner 10, lancé en 1973 vers Venus, et qui, profitant de la pesanteur de celle ci, prolongea sa propre orbite jusqu' à la planète Mercure. La sonde Ulysses mis à profit sa rencontre avec Jupiter afin de sortir de l'écliptique, et se placer dans une orbite passant à l'aplomb des deux pôles du soleil. Et la "sonde solaire," de la NASA, qui doit s' approcher à 4 rayons solaires du centre du soleil, virera autour de Jupiter en une trajectoire en épingle à cheveux. Un ardent défenseur des manœuvres aidées par la gravité, en vue de vols économiques entre Terre et Mars a été l'astronaute Buz Aldrin. Ses idées sont décrites dans l'article "Un autobus interplanétaire" de James Oberg et Buz Aldrin, p. 58-60, " Scientific américan," mars 2000. Un parallèle intéressant existe entre ces manœuvres de valse interplanétaire et le fonctionnement de la turbine à eau de Pelton. Plus de détails sur ceci dans la section 35a : Valse interplanétaire et turbine à eau de Pelton. Vers les étoiles |

Les croisements rapprochés avec les planètes ont une autre utilisation : l'effet de poussée sur toute fusée est considérablement amplifié à l'approche de celle ci. Un projet de mission, "Profile", sur la magnétosphère de la terre, utilise une douzaine de petits satellites, placés d'abord dans un "vaisseau mère" sur une orbite elliptique allongée. A chaque rapprochement (au "périgée") un satellite est expulsé, pas plus vite qu'un coureur à pied, et pourtant cette poussée est suffisante pour lui faire passer le périgée au tour suivant avec une heure de retard. Lors de ce nouveau passage, un nouveau satellite est éjecté, et ainsi de suite, à chaque approche du périgée. Finalement tous les satellites sont égrenés à une heure de distance sur une nouvelle orbite (dessin de droite), différant légèrement de celle du vaisseau - mère. Cela est réalisé par une poussée des plus douce, mais qui doit être fournie au bon endroit. |
|
Dans un futur lointain, l'humanité voudra probablement envoyer des robots explorateurs vers les étoiles éloignées, voyages qui peuvent demander des milliers d'années. Il y a bien longtemps que l'on a proposé d'obtenir la vitesse exigée en passant d'abord au ras du soleil, par un tir de fusée "au plus près". La moindre augmentation de vitesse près du soleil se traduit alors par une grande augmentation de la vitesse finale sur le trajet éloigné. Malheureusement, ceci exige d'aller très près du soleil, ou la sonde spatiale serait susceptible de fondre. Un objectif plus raisonnable pour se diriger vers une étoile serait peut être d'utiliser une comète, dont la trajectoire se prolonge aux confins du système solaire, et dont la glace peut fournir de l'hydrogène et de l'oxygène comme combustible des moteurs de fusée. De cette manière, on pourrait atteindre les étoiles les plus proches de la terre. Pour aller plus loin dans la galaxie, il faudrait des rencontres du type de celles proposées avec le soleil .Peut être pourrait - on localiser des étoiles naines, petites comme la terre et massives comme le soleil, dont certaines sont refroidies et obscures. Si oui, elles seraient une cible parfaite pour une telle manœuvre. Tout ceci n'est actuellement que pure imagination : mais l'humanité a le temps, son exploration de l'espace ne fait que commencer. |
En savoir plus :
"The Art of the Orbit" de Gary Taubes, Science, p. 620-2. vol 283, 29 January 1999. Une revue des orbites inhabituelles de l'exploration du système solaire."The Starflight Handbook" (sous titre: "A Pioneer's Guide to Interstellar Travel"), de Eugene F. Mallove and Gregory L. Matloff, John Wiley & Sons, 1989.
"Voyager 2" est actuellement sur sa sortie du système solaire. En misant sur la chance, un certain jour dans le futur, une civilisation étrangère pourrait trouver un message envoyé avec lui. Voir les détails ici
Revenir à la liste principale
Mail au Dr.Stern: stargaze("at" symbol)phy6.org
.
