La tangente est un outil de trigonométrie, liée au sinus et au cosinus. Sur ce site Web elle est étudiée en liaison avec le bâton en croix (Croix de Jacob).

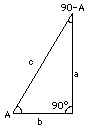
Vous savez déjà que les triangles rectangles sont à la base de la trigonométrie. Soit ABC un tel triangle (dessin) avec l'angle à 90° en C et (A, B) les angles aigus a, b et c sont les longueurs des trois côtés --a en face de A, b en face de B, et c le plus long, en face de C.

Deux proportions utiles sont liées à l'angle A (" fonctions trigonométriques ") :

Ces deux proportions concernent le grand côté c ("hypoténuse" en jargon mathématique), et puisque a et b sont plus petits que lui, ces fractions sont inférieures à 1. Nous ajoutons maintenant à notre collection deux fractions supplémentaires : la tangente et la cotangente:

la tangente de A

Une relation simple existe entre chacune d'elles et les deux autres déjà vues : Nous avons

Multipliez haut et bas par c (cela revient à multiplier la fraction par (c/c)=1) et on obtient :

Les calculatrices qui évaluent sinus et cosinus, et les tables dans les livres, donnent également les tangentes et les cotangentes.

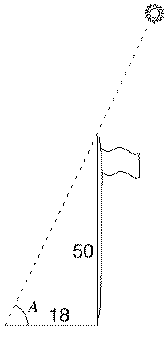
Une Application Simple

A l'aide d'une table de tangentes, vous pouvez maintenant rechercher les angles dont les tangentes tombent juste au dessus ou au dessous de cette valeur, et évaluer celle de A ("interpoler"). Les calculatrices possèdent habituellement une touche "tan" qui, si vous inscrivez l'angle, vous en donne la tangente. Mais beaucoup ont également une touche "tan ^-1" " qui fait l'inverse --La tangente,étant enregistrée, elle donne l' angle. (ce peut être la même touche, calculant tan^-1 si vous appuyez d'abord sur un bouton intitulé "mode spécial" ; tan^-1 est dite aussi "tangente inverse" ou "arctangente"). Dans notre exemple,

P.S.: La tangente à un cercle est la droite qui le frôle juste en un point. Si jamais vous vous demandez quelle est la relation entre "tangente" et trigonométrie, cliquer ici. .