Disclaimer: The following material is being kept online for archival purposes.

Although accurate at the time of publication, it is no longer being updated. The page may contain broken links or outdated information, and parts may not function in current web browsers.

Mappa del Sito
Matematica Indice
Glossario
Cronologia
Domande e Risposte (inglese)
Piani delle Lezioni (inglese)
#M-11a  Esercizi di Trigonometria

(M-11)  Come ricavare   sen(α+β),   cos(α+β)

Date le funzioni (senα, cosα, senβ e cos β), cerchiamo le formule che esprimono sen(α+β) e cos(α+β). La prima di queste formule è usata qui, nel calcolo dei punti di Lagrange L4 e L5.

Per favore verificate ogni passaggio nei calcoli prima di procedere!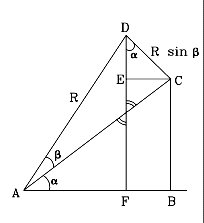

Come mostrato nel disegno, per ricavare la formula combiniamo i due triangoli rettangoli

    ABC che ha un angolo α
    ACD che  "   "     "       β
Il lato lungo ("ipotenusa") di ACD è AD=R. Perciò

    DC = R sen β
    AC = R cos β
In modo simile

    BC = AC sen α = R cos β sen α
    AB = AC cos α = R cos β cos α
Il triangolo ADF è rettangolo e ha l'angolo (α+β). Perciò

    R sen (α+β) = DF
    R cos (α+β) = AF

Iniziamo col ricavare il seno:

    R sen (α+β) = DF  =  EF + DE  =  BC + DE
  Si osservino nel disegno i due angoli opposti al vertice indicati con doppie linee: come tutti gli angoli di quel tipo, essi devono essere uguali. Ciascuno di essi è uno dei due angoli "acuti" all'interno del proprio triangolo rettangolo. Siccome la somma degli angoli acuti in un tale triangolo è di 90 gradi, gli altri due angoli acuti devono essere uguali. Ciò giustifica il fatto di chiamare α l'angolo vicino a D, così come disegnato in figura.

Nel triangolo rettangolo CED

    DE = DC cos α = R sen β cos α
    EC = DC sen α = R sen β sen α
Precedentemente è stato già mostrato che
    BC = R cos β sin α
    AB = R cos β cos α
Perciò

 R sen (α+β)  =  BC+DE  =  R cos β sen α + R sen β cos α

Eliminando R e riordinando α in modo che preceda β

   sen (α+β)  =  sen α cos β + cos α sen β

In modo simile, per il coseno

R cos (α+β) = AF = AB –FB = AB –EC =

        = R cos β cos α – R sen β sen α

Eliminando R e riordinando

   cos (α+β)  =  cos α cos β – sen α sen β

Applicazione di queste formule:  #34b   I Punti di Lagrange L4 e L5

#M-11a   Esercizi di trigonometria

Prossimo Argomento:  #M-12   La Tangente

Autore e Curatore:   Dr. David P. Stern
Ci si può rivolgere al Dr. Stern per posta elettronica (in inglese, per favore!):
                                stargaze("chiocciola")phy6.org

Traduzione in lingua italiana di Pietro Sauro

Aggiornato al 17 Settembre 2004

Above is background material for archival reference only.

NASA Logo, National Aeronautics and Space Administration
NASA Official: Adam Szabo

Curators: Robert Candey, Alex Young, Tamara Kovalick

NASA Privacy, Security, Notices