(14) I vettori
I vettori come estensione dei numeriL'idea dei numeri si è sviluppata molto gradualmente. Dapprima vennero gli interi positivi -- 1,2,3... (non lo zero, che è stata un'aggiunta molto più recente) per descrivere gli oggetti contabili, come le pecore, i giorni, i membri della tribù, ecc. Il concetto dei numeri negativi può essere stato originato da un'estensione della sottrazione, o forse dal denaro -- il denaro dovuto era una ricchezza "negativa", scritta in rosso nel registro contabile. Oggetti che potevano essere suddivisi, come per esempio le terre, portarono alle frazioni. Attorno al 500 a.C. uno studente di Pitagora dimostrò che il numero corrispondente alla radice quadrata di 2 non poteva essere espresso come una frazione; questo non aveva molto senso per quei tempi, per cui ancora oggi chiamiamo quei numeri "irrazionali". Con questi numeri, interi, frazioni e irrazionali, può essere descritto tutto ciò che ha una dimensione, una grandezza. Ma come facciamo a descrivere una velocità, che ha, oltre a una grandezza, una direzione? Con un vettore, naturalmente. Somma di vettoriLe velocità possono essere sommate. Supponiamo che un aeroplano voli a 200 km/ora con un vento in coda di 100 km/ora. Quanto velocemente si sposta rispetto al suolo? Facile: per ogni 200 km di percorso, il vento lo trasporta in avanti di altri 100 km, per cui la risposta è Graficamente, ogni distanza sul suolo, od ogni velocità, può essere rappresentata da una freccia che dà la direzione, e la cui lunghezza rappresenta la grandezza: per esempio, una freccia AB lunga 200 mm (millimetri) corrispondente al moto dell'aeroplano e un'altra BC, lunga 100 mm, nella stessa direzione, corrispondente al vento. Per sommare le due velocità, basta posizionare le due frecce, una di seguito all'altra, come nella figura più in alto, qui accanto.
e la "somma delle frecce" (figura centrale) ce lo conferma. Supponiamo adesso che la rotta dell'aereo sia diretta verso est, ma con un vento di 150 km/ora che soffia di lato verso nord-est: in che direzione si muoverà l'aereo, e quanto velocemente? L'intuizione questa volta non ci aiuta, ma il metodo della somma delle frecce funziona ancora (figura più in basso, non in scala). Come regola generale, la combinazione delle due velocità porta l'aeroplano, in un'ora, nello stesso punto che si raggiungerebbe se la prima velocità e poi la seconda agissero separatamente durante un'ora di tempo. Come ci si può aspettare, la direzione combinata corrisponde a una via di mezzo tra est e nord. Tutti i vettori possono essere addizionati in questo modo, come frecce collocate con la coda dell'una sulla punta della precedente. Esiste comunque anche un altro metodo, spesso più facile da usare, che verrà descritto più avanti.
Un modo molto più rapido è quello di scegliere due direzioni perpendicolari tra loro: con la notazione delle coordinate cartesiane, una direzione sarà chiamata la "direzione x" e l'altra la "direzione y". Si scompone quindi ogni vettore V in una "componente x" Vx lungo la direzione x e una "componente y" Vy lungo la direzione y.
Adesso abbiamo non 10 ma 20 vettori che devono essere addizionati, ma il lavoro è molto più facile. Di questi vettori, 10 sono allineati con la direzione x, e vettori nella stessa direzione (come le velocità con il vento in coda e contro vento nel precedente esempio dell'aeroplano) si sommano come numeri ordinari. Lo stesso vale per gli altri 10 vettori allineati con la direzione y. Il problema si riduce a una fila di ordinarie addizioni e sottrazioni (vettori orientati in verso opposto hanno il segno negativo), e soltanto l'ultima fase -- quella di sommare tra loro il totale della direzione x con il totale della direzione y -- richiede un procedimento di somma di vettori.
Riprendiamo l'esempio precedente dell'addizione di vettori -- un aeroplano che vola verso est a 300 km/ora (la sua velocità anemometrica, cioè la sua velocità rispetto all'aria), mentre un vento a 150 km/ora soffia verso nord-est. Il triangolo che rappresenta la somma vettoriale di questo esempio si trova in fondo alla prima figura di questa sezione.
Sia la direzione x quella verso est e la direzione y quella verso nord. Allora, le componenti (x,y) della velocità sono, in km/ora,
Questo risultato fornisce la velocità totale V. Per il teorema di Pitagora,
e quindi la grandezza di V è approssimativamente 420 km/ora, dove l'angolo acuto nel punto A della figura (che pure chiameremo A) soddisfa la relazione
Da cui risulta che A è circa 16,62 gradi. (c) Il piano inclinatoQuesto esempio ci riporta all'esperimento di Galileo. Supponiamo di avere un piano leggermente inclinato a un angolo s (ved. disegno qui sotto) e su di esso un blocchetto ben lubrificato, pronto per essere fatto scorrere sul piano (Galileo aveva usato delle palline fatte rotolare sul piano inclinato, ma, se questo esperimento era più facilmente realizzabile, era però più difficile da calcolare, poiché l'energia cinetica viene suddivisa tra quella del moto traslatorio e quella del moto rotatorio della pallina). Se l'attrito è trascurabile, quanto velocemente il blocchetto scivola giù?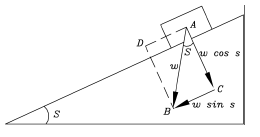
La forza di gravità che agisce sul blocchetto (tale forza ha un nome: è il peso W del blocchetto) può essere rappresentata dalla freccia verticale AB di lunghezza W, orientata verso il basso. Questa non è però la direzione in cui il blocchetto può accelerare. Il vettore AB deve essere scomposto in due forze perpendicolari tra loro:
|
Ulteriori approfondimenti:
Un'altra elementare introduzione ai vettori.Il prossimo argomento: #15 L'energia
Cronologia Glossario Torna alla pagina iniziale
Autore e Curatore: Dr. David P. Stern
Ci si può rivolgere al Dr. Stern per posta elettronica (in inglese,
per favore!):
stargaze("chiocciola")phy6.org
Traduzione in lingua italiana di Giuliano Pinto
Aggiornato al 14 Agosto 2005


