(22d) El vuelo del Aeroplano
-- ¿Qué tan Alto? ¿Qué tan Rápido?
|
Un avión se mantiene en las alturas debido al flujo de aire sobre y bajo su ala. Ese flujo crea una fuerza de levantamiento hacia "arriba" que se opone a la gravedad, la cual evita que el aeroplano caiga.
Aerodinamismo y ArrastreLa sección transversal del "perfil" del ala de un aeroplano debe cumplir con dos condiciones. Primero, su parte trasera debe terminar en forma ahusada o achaflanada hasta convertirse en una orilla delgada como una cu–a. Ese es el lugar en donde los dos flujos de aire, el de arriba y el de abajo del ala, deben unirse, y tal "aerodinamismo" asegura que dichos aires se unan suavemente, sin flujos turbulentos, los cuales incrementarían la resistencia al aire. En contraste, un paracaídas abierto, cuya parte trasera en una semiesfera, crea una gran cantidad de turbulencia detrás de el y tiene una gran resistencia; las trocas o camionetas que terminan de manera abrupta en una puerta alta para la carga encuentran de manera similar una resistencia relativamente alta al aire.
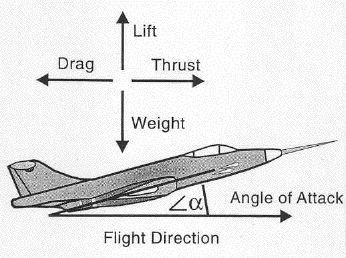El aerodinamismo reduce la resistencia al aire ("arrastre" en aviación). Los experimentos han mostrado que la fuerza de arrastre D (las letras en negritas no se usan aquí para distinguir vectores) incrementa con la velocidad v, de hecho, se incrementa de la forma v2. También es proporcional a la densidad del aire d; todos los otros factores que agregamos aquí en un coeficiente A, el cual es proporcional al área del ala y depende de la forma de su área transversal (aquí es donde entra en consideración el aerodinamismo) y en el "ángulo de ataque" con el cual se enfrenta al flujo del aire (ángulo=cero cuando el ala está alineada con el flujo de aire).
La proporcionalidad del arrastre de una ala aerodinamizada con respecto a v2 fue encontrada a partir de observaciones, pero también puede ser soportada por el áspero (hecho a mano) argumento de abajo. !Sígalo con calma!. El ala de un aeroplano de frente a una corriente de aire pierde energía en su mayoría por hacer a un lado el aire cuyo espacio procede a ocupar. Si el patrón de las líneas de flujo alredor del ala en baja y alta velocidad es la misma (razonablemente cierto), cuando v se duplica, la velocidad del aire desplazado hacia los lados también se duplica, y tan solo por este proceso, la energía (cinética) que se le imparte, proporcional a mv2, deberá incrementarse 4 veces. ¿Qué hay con m? Con la velocidad duplicada, el ala avanza el doble de la distancia que con anterioridad por cada segundo, de manera que la masa de aire m desplazada también se duplica. La proporción general en la cual la energía es impartida por el ala al aire circundante, por lo tanto, se incrementa 8 veces. Esa proporción también deberá concordar con el trabajo mecánico realizado cada segundo por la fuerza D (es decir, la potencia requerida): esta debe también incrementarse 8 veces. Dado que la distancia cubierta por segundo es v, el trabajo hecho cada segundo es Dv. Si v se duplica y Dv se incrementa 8 veces, entonces D debe incrementarse 4 veces , un incremento proporcional a v2. LevanteEl segundo requerimiento es que el ala produzca levantamiento, una fuerza hacia arriba que mantiene el aeroplano en flotación. Para reducir el levantamiento, el ala no debe ser simétrica, debe ser plana en la parte inferir pero elevándose en una curva en la parte superior. Esa forma incrementa la velocidad del flujo del aire en la parte superior, lo cual reduce la presión de aire allí, y cuando la presión en la parte inferior del ala es mayor que la presión de la parte superior, el resultado neto es una fuerza hacia arriba. [Un ala simétrica en la parte superior y en la inferior pero enfrentando una corriente de aire con un ángulo de ataque moderado, también satisface esta condicíon no simétrica.]Los investigadores desde la época de los hermanos Wright han usado túneles de viento para probar los modelos de diferentes perfiles de alas, y de esta manera han identificado secciones transversales adecuadas para varios tipos de vuelo. También han encontrado mediante observaciones que la fuerza de levantamiento producida por un ala era más o menos proporcional a la densidad d del aire y al cuadrado de la velocidad v del flujo de aire sobre ella:
Aquí L es el levantamiento en (digamos) Newtons, d es la densidad del aire (aproximadamente 1.3 kg/metro3 al nivel del mar y v puede estar en metros/seg, millas/hora o km/hora, lo que uno prefiera. El factor B depende del perfil del ala, la longitud del ala y su anchura: un ala más larga obviamente le da un levante más grande. También, el levante es proporcional al arrastre: los aeroplanos normalmente vuelan en el "ángulo de ataque" (definido anteriormente) lo cual les da la operación más económica, cuando la relación levante/arrastre es lo mayor posible. Ese "mejor" valor depende del dise–o del ala y puede variar desde 10 (y aún menos en aviones de guerra) hasta 50 (en deslizadores de alto desempe–o). Se puede incrementar el levante, aumentando el ángulo de ataque (como se realiza con un papalote o cometa), pero a un costo de tener un arrastre mucho más grande. Aún más, si el ángulo es demasiado grande, el flujo ordenado sobre el viento se interrumpe y el ala "pierde estabilidad, " perdiendo repentinamente mucho de su levante. Muchos accidentes de aeroplanos han sido rastreados a repentinas pérdidas de estabilidad.
¿Qué tan Alto? ¿Qué tan Rápido?Suponga que dise–a una avión pesando W kilogramos (aproximadamente 10W Newtons). En un vuelo nivelado, por supuesto, el levante debe balancear el peso del avión
El valor de W depende de B, en otras palabras, el ala debe ser suficientemente larga, suficientemente ancha y suficientemente eficiente para mantener el peso W del avión cargado en el aire. ¿Qué tan alto y qué tan rápido deberá volar el aeroplano? los pasajeros quieren llegar a su destino rápidamente, de manera que los dise–adores se enfocan a una alta "velocidad de crucero". Sin embargo, los pasajeros también valúan el tener aterrizajes seguros, y por lo tanto, la velocidad de aterrizaje debe también de ser baja. La velocidad es la razón principal de porqué los aviones vuelan a una altura superior a los 30,000 pies o cerca de los 10 kilometros. La densidad del aire decrementa aproximadamente la mitad por cada 5 km de altura, de manera que a los 10 km, d es aproximadamente 1/4 de su valor al nivel del mar y un avión puede duplicar su velocidad para generar el mismo levante, con el mismo arrastre D (el cual, como se mostró, también se incrementa de acuerdo a dv2). La razón principal de que las aeronaves tengan cabinas presurizadas es para que les permita volar más alto, para poder volar más rápido. ¿Qué tan rápido? El límite práctico parece estar alrededor de las 600 mph (960 km/hr). Entre más se acerque a la velocidad del sonido (1200 km/h = 746 mph, varía con la temperatura), el flujo de aire arriba del ala crea frentes de choque, lo cual incrementa el arrastre y reduce el levante. Aún para acercase a dicha velocidad límite, se requieren alas echadas hacia atras.
Aterrizaje SeguroUna velocidad de 600 mph (960 km/hr) a una altura de 10 km parece implicar un aterrizaje a la altura del nivel del mar a una velocidad de 300 mph (480 km/hr) (d es 4 veces mayor, de manera que v se puede disminuir a la mitad). Eso es aún demasiado rápido, inclusive el Transbordador Espacial se dice que aterriza a 270 mph (432 km/hr). Uno puede volar a 70,000 feet (about 20 km) de la manera que el avión de reconocimiento U-2 lo hace, y aterrizar (aún sin cambiar el ángulo de ataque) a 150 mph (240 km/hr). Sin embargo, para crear el levante necesario en el aire tenue de dicha altura, B debe ser mucho mayor, esto es, el ala debe ser mucho más grande, o si no, el peso W debe ser reducido (o ambos). Eso fue hecho para el U-2, un avión de peso ligero con un ala muy larga y eficiente, pero tal dise–o no trabajaría en la escala de un avión comercial.La solución práctica es incrementar el ángulo de ataque durante los aterrizajes, y temporalmente incrementar el tama–o del ala. Si alguna vez se ha sentado cerca de la ventana de un avíon al aterrizar, puede haber notado las superficies adicionales del ala deslizándose hacia afuera durante la aproximación final, para proveer más levante, y si observara dicha nave desde la tierra, notaría que esas superficies se extienden hacia abajo desde el ala, en un ángulo más pronunciado. Todo esto por supuesto que hace el arrastre mucho más grande, pero un avión en aterrizaje debe de cualquier manera deshacerse de su velocidad adicional.
Todo esto permite que el aeroplano aterrice a una velocidad aproximada de 150 mph (240km/hr). El aterrizar es definitivamente una maniobra de precisión, en la cual el aeroplano (idealmente) se queda sin velocidad del viento justo antes que las ruedas toquen piso. Radares de descenso y otras ayudas de navegación hacen esto posible, miles de veces al día.
Inicialmente, la intención era tener una cabina presurizada y volar a 25,000 ft., pero limitaciones de peso impidieron eso, de manera que un vuelo más lento y de menor altura fue llevado a cabo, tomándole 9 días. El peso de despegue del "Voyager" era de 9700 libras, y para levantar un avión tan pesado, utilizó dos motores, uno empujando y otro jalando, para lacanzar la velocidad requerida de 138 mph.
A medio vuelo, gracias a estar consumiendo combustible, se requería cada vez menos levante, por lo tanto se apagó un motor, y la velocidad del viento fuer permitida a reducirse a 79 mph, y para evitar que se redujera aún más, la atitud del vuelo se incrementó a 11,000-12,000 pies. Como resultado la segunda mitad del vuelo fue mucho menos veloz que la primera, y más difícil para los pilotos, quienes no habían dormido. No tenían, sin embargo, otra opción, el volar más rápido les hubiera requerido un ángulo de ala menos eficiente, y hubieran gastado demasiado combustible.
|
Nota: La historia del vuelo sin escalas alrededor del mundo se relata en "Voyager" por Jeana Yaeger,
Dick Rutan y Phil Patton, viii + 337 pp, Alfred A Knopf, New York, 1987.
Siguiente parada: #23 Marcos de Inercia Acelerados: Fuerzas de Inercia
Timeline Glosario De regreso a la Lista Maestra
Autor y Curador: Dr. David P. Stern
Correo al Dr. Stern: stargaze("at" symbol)phy6.org .
Traducción al Español por Horacio Chávez
Última Actualización 22 de Septiembre de 2004
