"Ingravidez"

donde el peso del astronauta  mg sobre la superficie de la Tierra a r = R_E está ajustado para la gran distancia a la izquierda. Esta es la misma ecuación que se usó para demostrar el estudio de la gravedad de Newton. Sin embargo, también se puede escribir como

Esto puede interpretarse como una afirmación de que en el marco de referencia del astronauta, todos los cuerpos están sometidos a dos fuerzas, gravedad y fuerza centrífuga y las dos están en perfecto equilibrio sumando cero. 

Se afirma algunas veces que los astronautas en el espacio están en condiciones de "gravedad cero", pero normalmente están, todavía, bajo la influencia de la gravedad de la Tierra. Es cierto que los astronautas no tienen tendencia a caer hacia la Tierra, pero por una razón diferente que puede explicarse de una de las dos formas siguientes:

1. La gravedad se utiliza totalmente para proporcionar la aceleración continua (la1ª de la ecuaciones); ó
2. La fuerza de la gravedad está equilibrada perfectamente con la fuerza centrífuga (2ª ecuación). 

Simulación de "Cero g" en un Aeroplano

Luego la ecuación de movimiento de un objeto sujeto a F solamente es

La aceleración a es la que experimenta una nave espacial, vista desde el marco fijo de la Tierra. En una órbita circular de radio r equivale a v²/r, mientras que en una órbita elíptica puede tener una magnitud  y dirección diferentes, que también pueden calcularse. Lo más importante a advertir aquí es que un astronauta dentro de la nave espacial esta sujeto a la misma gravedad y por lo tanto experimenta la misma aceleración que la propia nave. Viendo el movimiento del astronauta en el marco de la nave en movimiento, no es atraído hacia el suelo de la cabina ó en cualquier otra dirección, y, por lo tanto, tiene la impresión de que la gravedad ha sido eliminada.

 Suponga que en vez de eso, el astronauta va dentro de una cabina en caída libre, cercana a la superficie de la Tierra. Ahí, también

pero como r es muy cercano a 1 R_E, podemos fijar que el radio es igual a 1 y tener simplemente

La cabina cae con una aceleración g, pero el pasajero también cae con la misma aceleración, luego, de nuevo, no existe una fuerza que empuje al pasajero hacia el suelo de la cabina. Observando la cabina que le rodea, el pasajero tiene la impresión de que la gravedad no existe.

 No existe diferencia si la cabina comienza con una velocidad constante, p.e. lanzada hacia arriba con una velocidad inicial u y con una velocidad horizontal inicial w, porque ninguna de ellas afecta a las fuerzas y aceleraciones. La cabina y el pasajero estarán acelerados hacia abajo a una a=g, creando la ilusión de gravedad cero.

 Si este experimento se reproduce en la realidad, esa ilusión y la cabina se harán añicos pronto al entrar en contacto con el suelo. Además, la resistencia del aire rápidamente reduce la aceleración de la cabina por debajo de g. Dentro el pasajero, aún sometido a a=g, sobrepasará a la cabina, en un proceso que aparecerá, en el marco de la cabina, como un retorno parcial de la gravedad.

 Sin embargo, el mismo experimento se puede realizar de forma segura en un avión de alta velocidad, que podrá vencer cualquier resistencia del aire con el empuje de sus motores. Siguiendo una ruta parabólica programada similar a la de un proyectil sujeto solo a la gravedad, este avión puede crear, para un tiempo limitado, un entorno de gravedad cero dentro de la cabina.

 La NASA ha realizado esto con un avión KC-135, un avión a reacción de 4 motores, apodado "La Cometa del Vómito" porque su repentina transición a cero-g hace que algunos pasajeros se mareen. El avión puede producir un entorno temporal de cero-g en su cabina, y se usa para el entrenamiento de los astronautas y para experimentos cortos en cero-g. El espacio de carga dentro de él está completamente acolchado, y se puede mantener una ilusión de gravedad cero durante 20-30 segundos.

La Fuerza de Coriolis

Estación espacial con astronave volando de visita (Von Braun's, de los años  1950's)

La película de ciencia ficción "2001: Una Odisea del Espacio" presentó una estación espacial giratoria, cuya rotación suministraba a la tripulación "gravedad artificial". Era una estructura en forma de rueda, con radios huecos que conectaban la rueda a una cabina en el centro (dibujo). La cabina del centro era donde se producía la transferencia entre la estación y la nave visitante. Pulse aquí para ver más sobre este diseño.

Teniendo tal rotación, se produce algo parecido a la gravedad, con el "abajo" hacia el exterior (Larry Niven amplía este concepto en su imaginativa novela de ciencia ficción "Ringworld" y sus secuelas). Cuando se calcula sus efectos es más simple usar el marco de referencia de la estación y añadir una fuerza centrífuga a todas las demás fuerzas. 

No obstante, cuando nos movemos en este medio giratorio, especialmente el movimiento arriba y abajo en los radios, se encuentra una fuerza adicional, denominada en honor del francés Gaspard Gustave de Coriolis (1792-1843). 

Imagine a un astronauta moviéndose a lo largo de uno de los radios, desde el punto A al punto B en el dibujo, más probable, ascendiendo una escalera, con su movimiento en contra la "gravedad artificial" de la estación. En cualquier punto, como se ve desde el marco de referencia del mundo exterior, el astronauta también gira alrededor del eje de la estación. 

En ambos puntos A y B, la rotación es en la misma dirección, pero en B es menor, porque ese punto está más cerca del eje de rotación y por lo tanto describe un círculo pequeño. ¿Que ocurre en B con la velocidad extra que el astronauta tenía en A?. De acuerdo a la 1ª ley de Newton, libremente aplicada, el astronauta tenderá a mantener esa velocidad extra y por tanto será empujado contra el lateral del radio (dirección de las flechas). Este empuje es la fuerza de Coriolis. Cuando el movimiento es en la dirección opuesta, desde B a A, la dirección de la fuerza es... ¿la misma ó la inversa? ¡Trabájela usted mismo! 

Remolinos de Agua en la Pileta del Baño

El principio físico es acertado, pero el efecto real es tan microscópico que es improbable que se observe en las piletas. Por otro lado, el mismo efecto es muy importante en los remolinos a gran escala de la atmósfera, en los huracanes y tifones, así como en los modelos del tiempo ordinarios. 

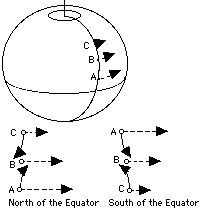
La Tierra, cuando se ve desde encima del polo norte, gira antidextrogiro (contra las agujas del reloj). Imagine 3 puntos en el hemisferio norte, en la misma longitud geográfica (dibujo), A cerca del ecuador, B algo más hacia el polo y C aún más hacia el polo. Cada uno de esos puntos cubre en un día un círculo completo alrededor del eje de la Tierra: A tiene el círculo mayor, recorre la mayor distancia y por tanto se mueve el más rápido, B con un círculo menor se mueve más lento, y C es aún más lento. Los puntos se vuelven a dibujar a la derecha en una escala mayor, con flechas pegadas para indicar las direcciones y magnitudes de sus velocidades. 

Imagine ahora que por alguna razón se desarrolla en el punto B, en la atmósfera, un area de baja presión. El aire tenderá a fluir hacia B desde A y C, pero cuando ocurre esto, tiende a mantener su velocidad de rotación, como el astronauta del ejemplo precedente. Así, el flujo real desde A (flecha de puntos) finaliza delante de B, desviado hacia la derecha (en el marco giratorio), y el flujo desde C finaliza rezagado detrás de B, desviado hacia la izquierda. El resultado es el mismo que la adición de un remolino antidrextrogiro alrededor de B. 

Próxima Etapa --El Sol: #S-1. La Luz del Sol y la Tierra

Próxima Etapa --Vuelo espacial: #25 Fundamentos del Cohete

Author and Curator:   Dr. David P. Stern
     Messages to Dr.Stern:   stargaze("at" symbol)phy6.org   (English, please) .

Spanish translation by J. Méndez

Last updated 13 December 2001