|
|
|
|
|
|
|
|
(M-9) Deriving Sines and Cosines
|
Deriving the sine or cosine of an arbitrary angle takes a bit more math than is covered here. However, deriving them for a few special angles is relatively straightforward. Complementary anglessNote first of all that a right-angled triangle contains two angles. Since all three angles (in any triangle) add up to 180°, the two sharp angles add up to 90°. It follows that if one of the angles is of A degrees, the other one (its "complementary angle") is (90°− A). The sine and cosine were defined as the following ratios: sin A = (side opposite to A)/(long side) Because the side opposite to A is the one adjacent to (90°– A), it follows that the sine of one angle is the cosine of the other, and vice versa: sin A = a/c = cos (90° –
A) This is a great help: deriving (for instance) the sine and cosine of 30°also gives us, as a bonus, the sine and cosine of 60°. (1) A = 45°
If A = 45°, then also (90° –
A) = 45°, and therefore
sin2 45° = 1/2
sin 45° = √2/√4 = √2/2
(2) A = 30°, (90° – A) = 60°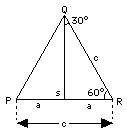
Consider the triangle PQR (drawing) with all three angles equal to 60°. By symmetry, all three sides are equal too (a more rigorous proof exists, but we skip it). Drop a line QS perpendicular to PR: it divides the big angle into two right-angled triangles with sharp angles of (30°, 60°), which is the kind we are interested in. By symmetry, the triangles are of equal size and shape ("congruent") and therefore (skipping another proof)
In the notation of the drawing
a/c = 1/2 = sin 30° = cos 60°
Subtract 1/4 from both sides
cos 30° = √3/ √4 = (√3)/2 = 1.7320508/2 cos 30° = 0.8660254 = sin 60°
(3) A = 90° , (90° – A) = 0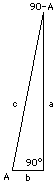
It would be rather hard to draw a right-angled triangle with a second angle of 90° inside it, because the third angle then has to be 0°. But we can visualize this strange triangle as the limiting case of long skinny triangles with an angle A that is very steep and and its complement (90° –
A) very small (drawing). In the limiting case
cos A = b/c = 0 and since 1 = sin2A + cos2A = sin2A + 0 it follows that sin2A = 1 sin A = 1 Therefore cos 90° = sin 0° = 0 The full table then reads |
| A | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| sin A | 0 | 0.5 | 0.707107 | 0.866025 | 1 |
| cos A | 1 | 0.866025 | 0.707107 | 0.5 | 0 |
|
You should be able to draw a fairly good graph of sinA and cosA using the above points (4) Postgraduate: A = 15°, (90° – A) = 75°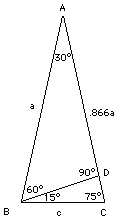
The preceding derivations and table are standard fare in practically any course or text on trigonometry. You notice however the gaps between 0° and 30°, and between 60° and 90°. If we want the angle A to grow in equal steps of 15o, we still need the sine and cosine of 15° and 75°. Are you interested? Here is how it can be done; hold on to your calculator! Draw a triangle ABC, with the angle A equal to 30° and the two bottom angles each equal to 75°. Then draw line BD perpendicular to AC (see drawing on the right). By symmetry, the sides AB and AC are of the same length; let that length be denoted by the letter a. The triangle ABD has angles of 90, 60 and 30 degrees, and is therefore of the kind examined earlier. We get BD = a sin 30° = 0.5 a Then DC = AC – AD = a – 0.866025 a = 0.133975 a  Now look at the triangle BDC: its two larger angles equal 90° and 75°, forcing the remaining angle to be equal to 15°. Using the theorem of Pythagoras, if the long side is denoted c, we get
BD2 + CD2 = c2 = (0.5 a)2 + (0.133975 a)2 Taking the square root c = 0.517638 a From that, to 5 decimals (and involving the complementary angle of 75° as well) sin 15° = 0.133975/0.517638 = 0.25882 = cos 75° Now go and draw your graph! |
Next Stop: #M-10 Going Past 90 Degrees
Author and Curator: Dr. David P. Stern
Mail to Dr.Stern: stargaze("at" symbol)phy6.org .
Updated 25 November 2001 Edited 28 October 2016
