The tangent is a tool of trigonometry, related to the sine and cosine. On this web site it is used in connection with the cross staff.

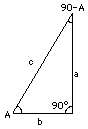
You already know that right angled triangles are basic to trigonometry. Let ABC be such a triangle (drawing) with C = 90° the right angle and (A, B) the sharp ("acute") angles. Also, let a, b and c be the lengths of its three sides--a of the side across from A, b of the one across from B, and c the longest one, across from C.

Two useful ratios associated with the angle A ("trigonometric functions of A") are

Both these ratios involve the long side c ("hypotenuse" in mathspeak), and since both a and b must be smaller than that side, these ratios are always numbers less than 1. We now add two more ratios to our collection--the tangent and the cotangent:

The tangent of A

A simple relation exists between this pair and the earlier ones. We have

Multiply top and bottom by c (it is the same as multiplying the fraction by (c/c)=1) and get

The calculators which give sines and cosines, and the books which tabulate their values, are also able to give tangents and cotangents.

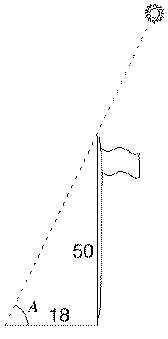
A Simple Application

If you have a table of tangents, you can now look for the angles whose tangents just above and just below that value, and estimate where between them A should be ("interpolate"). Calculators usually have a button "tan" which, if you punch in the angle, gives you the tangent. But many also have a button "tan ^-1 " which does the reverse--given the tangent, it brings up the angle. (It may be the same button, deriving tan^-1 if first you hit a colored "special mode" button; tan^-1 is also called "inverse tangent" or "arc-tangent"). In this example,

P.S.: A tangent to a circle is a line grazing it at just one point. If you ever wondered how the name "tangent" entered trigonometry, click here.