(34) Orbites dans l'Espace
Orbites SynchronesToutes les orbites de l'espace obéissent aux lois de Kepler et de Newton. Si l'orbite est circulaire, on peut ainsi formuler la troisième loi de Kepler, comme déjà vu : T = 5063 secondes R3/2 = 5063 secondes R * SQRT(R) avec T la période orbitale, * marquant la multiplication, R le rayon de l'orbite en unités de rayon de la terre (= 6371 kilomètres) et SQRT(R) la racine carrée de R.
On en déduit que pourT = 86400 sec = 24 heures, R = 6.6 rayons de la terre. S'itué à cette distance, un satellite équatorial présente une période de 24 heures et reste au-dessus du même point de l'équateur de la terre, puisque la terre tourne en même temps. Une telle orbite est idéale pour un satellite de communication, parce les " paraboles " qui le détectent n'ont alors pas besoin de le suivre dans le ciel, mais peuvent rester dans une direction fixe . L'auteur britannique de science-fiction Arthur Clarke a eu le premier l' idée de l'utilisation de cette orbite "synchrone", bien avant les premiers satellites artificiels. Clarke a écrit ultérieurement le livre "Fontaines du paradis" (situé au Sri Lanka, où il s'était rendu) dans lequel des câbles minces relient des satellites synchrones à la terre. Du matériel assez résistant et assez léger pour ce genre de câble n'existe pas, loin de là, et c'est probablement impossible ; mais il a écrit une excellente histoire. Environ 200 satellites sont maintenant sur orbite synchrone, en partie propriété des états, pour leur utilisation personnelle. Beaucoup sont gérés par des compagnies de télécommunication. |
Rentrée AtmosphériqueLa formule de Kepler s'applique également au mouvement elliptique, en remplaçant R par le demi grand axe " a " de l'orbite. Cependant, après un certain temps, les orbites diffèrent de l'exact tracé Keplerien en raison de forces additionnelles, telles que l'attraction de la lune ou du soleil. Pour des ellipses allongées, cela fait osciller de haut en bas le point le plus rapproché de l'orbite ("périgée"), qui finalement rase l'atmosphère, entraînant la perte du satellite. Le frottement atmosphérique provoque également tôt ou tard la rentrée des satellites de faible altitude: en perdant de l'énergie, ils descendent de plus en plus vers l'atmosphère, atteignant finalement les régions plus denses des couches supérieures, où ils brûlent. Ce fut le destin de la station spatiale Skylab en 1980 : La NASA avait espéré se servir de la navette spatiale pour la remonter sur une orbite plus élevée, mais la navette n'était pas encore prête. Entre temps, le cycle de 11ans des taches solaires était arrivé à son maximum, avec plus d'intensité que la NASA ne l'avait prévu, apportant davantage de rayons X solaires et de rayonnements ultraviolets extrêmes. Les couches les plus élevées de l'atmosphère absorbent ces rayonnements, ce qui les réchauffe, et les fait se dilater, surtout lors du "maximum solaire". Cette expansion a élevé en hauteur la résistance de l'air ("drag ") opposée à Skylab et a causé sa perte. Le renflement de la terreSi la terre était une sphère parfaite, sa masse serait en conséquence exactement centrée et le calcul des orbites amènerait à constater que si les forces en jeu sont à distances égales de la terre, elles sont tout à fait identiques. En réalité, il faut compter avec la force centrifuge, produite par la rotation de la terre, qui de plus n'est pas tout à fait sphérique, puisque plus large de quelques kilomètres à l'équateur qu'aux pôles. Cela modifie les orbites des satellites et doit être pris en considération. Si le plan de l'orbite est incliné par rapport à l'équateur, le bombement équatorial le fait tourner lentement autour de l'axe de la terre : une ligne perpendiculaire au plan de l'orbite décrit graduellement un cône. Cette rotation crée une situation particulière dont on peut tirer profit. |
|
En théorie, l'orbite d'un satellite est fixe dans l'espace, mais en fait son orientation change constamment par rapport au soleil, comme la terre qui tourne aussi autour de celui ci. Par exemple, prenons un satellite en basse altitude, dont le plan orbital contient l'axe de la terre (c.-à-d. qu'il passe au-dessus des pôles nord et sud).En juin, ce plan s'avère être exactement dans le sens aube-crépuscule, c.-à-d. à la séparation jour - nuit de la terre, alors qu'en septembre il passe en direction midi-minuit, une rotation de 90 degrés. Notez que l'orbite de juin est ensoleillée pendant 24 heures, mais pas celle de septembre. | 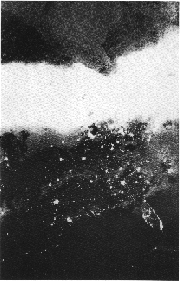
|
|
Toutefois, les plans de certaines orbites, passant juste à quelques degrés des pôles, tournent sur elles même en un an, en raison du bombement de la terre. De telles orbites,synchrones du "soleil", peuvent constamment faire face au soleil, ou se situer toujours à minuit. Ce type d'orbite concerne les satellites DMSP ",(la photo ci contre, une aurore au-dessus des Grand Lacs, a été prise par un de ces satellites; notez la Floride, à droite, en bas),de même que Magsat. Les satellites d'observation de la terre tels que Landsat et SPOT (Satellite Pour l'Observation de la Terre) fonctionnent également avec des orbites synchrones au soleil, ce qui permet de prendre des photos journalières aux mêmes heures . Sans cela, les différences dans les ombres peuvent compliquer leur interprétation. Points de Lagrange |
| Selon la 3ème loi de Kepler, un vaisseau spatial circulant autour du soleil sur un cercle de rayon plus court que celui de la terre aura aussi une période plus courte et se déplacera plus rapidement. Si il est lancé de la terre, il s'éloignera sans cesse de celle ci. Pourtant il y a une façon de les stabiliser l'un par rapport à l'autre. | 
|
Note additive, Juin 2003
Alors que les points de Lagrange furent la base historique de l' étude détaillée du problème des trois corps, d' autres orbites sont maitenant connue, en particulier une orbite présentant une figure en huit, et qui est stable. Voir Ici. |
Croisière dans le système solairePour échapper à la terre, un vaisseau spatial a besoin de la vitesse élevée de 8 km/s pour graviter en orbite basse de la terre, 11.2 km/s pour s'en échapper tout à fait. La seule manière connue d'obtenir de telles vitesses est de se servir de fusées. Mais lorsqu'un vaisseau spatial échappe à l'influence de la terre, il est encore retenu par celle du soleil. N'étant plus retenu par la terre, il adopte une orbite autour du soleil, à peu près à la même distance qu'auparavant. En conséquence, il lui faut une vitesse supplémentaire pour se déplacer dans le système solaire. L'objet le plus difficile à atteindre est le soleil lui-même. Un vaisseau spatial imaginaire, libéré de la terre, se déplacerait autour du soleil à environ 30 km/sec, comme la terre. La seule façon d'atteindre le soleil est d'annuler de façon ou d'une autre cette vitesse; par exemple, à l'aide d'une fusée permettant d'obtenir 30 km/s en direction opposée : dans ce cas, le vaisseau spatial tomberait directement vers le soleil. Ceux qui proposent d'envoyer des charges nucléaires directement par fusée sur le soleil ne semblent pas s'y connaître beaucoup en orbites ! Etant donné, la grande difficulté qu'il y a à donner à un vaisseau spatial les 8 km/s seulement nécessaires pour une orbite basse de la terre, la grande puissance exigée pour les fusées destinées à atteindre les planètes éloignées est un obstacle sérieux. Heureusement, il est souvent possible de profiter de l'attraction gravitationnelle des planètes pour aider aux manœuvres, comme cela sera présenté dans une prochaine section. |
Revenir à la liste principale
Mail au Dr.Stern: stargaze("at" symbol)phy6.org
.

