(M-7) Trigonométrie : Quelle utilité ?
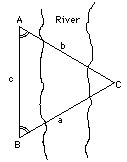
Le problème de base de la trigonométrie est à peu près celui ci : Vous vous tenez sur la rive d'un fleuve large et vous voulez savoir par exemple la distance d'un arbre de l'autre coté, désigné sur le schéma par la lettre C (pour simplifier ignorons la 3ème dimension). Comment faire sans traverser réellement le fleuve? La démarche habituelle consiste à planter deux poteaux aux points A et B, et avec un décamètre ou une chaîne d'arpenteur et à mesurer la distance c qui les sépare ("la ligne de base"). |
| Remplacez ensuite le poteau A par une lunette d'arpenteur comme celui de la figure ("théodolite"), munie d'un plateau divisé en 360 degrés permettant de repérer sa direction ("azimut"). En visant successivement l'arbre puis le poteau B, vous obtenez l'angle A du triangle ABC par soustraction des chiffres lus sur le plateau d'azimut. A partir du point B on mesure l'angle B de façon analogue. La longueur c de la ligne de base et les deux angles A et B sont suffisantes pour tout connaître sur le triangle ABC, assez, par exemple, pour construire un triangle de même taille et de même forme sur un terrain identique. La trigonométrie (trigon = triangle) était à l'origine l'art de préciser uniquement par le calcul les informations absentes . Avec suffisamment d'informations, la trigonométrie vous permet de calculer les dimensions et les angles d'un triangle préalablement défini. |
|
Note: Un résumé très lisible, avec l'histoire de William Lambton, le concepteur de cette mission, peut être trouvé dans "The Great Arc : The Dramatic Tale of How India Was Mapped and Everest Was Named" de John Keay, 160 pages reliées, Harper and Collins, Sept. 2000.
|
En savoir plus:
Au sujet de l'appellation du Mont Everest : naming of Mt. Everest.
Chronologie
Glossaire
Aide mathématique
Revenir
à la liste principale
Mail au Dr.Stern: stargaze("at" symbol)phy6.org

