(M-8) Que signifient sinus et cosinus
|
Les triangles ont des formes très diverses. Il serait difficile de classifier des triangles selon des formes arbitraires, mais il faut remarquer que tout triangle ABC peut toujours être divisé en triangles rectangles, des triangles dont un angle est égal à 90°. Il sont plus faciles à manipuler. 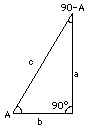
La somme des trois angles intérieurs d'un triangle est égal à 180° (nous n'en ferons pas la démonstration) et il s'en suit que dans un triangle rectangle la somme des angles aigus A et B vaut, puisque : A + B + 90° = 180° Soustraction de 90° des deux côtés : A + B = 90° Si on ne connaît que l'angle A, l'autre angle B est complètement déterminé (il est égal à 90°–A), et donc on connaît aussi la forme du triangle, mais cependant pas sa taille. Désignons les côtés d'un triangle par (a,b,c), en correspondance avec le nom de l'angle qui lui fait face L'angle A ne détermine pas la longueur d'un côté, mais fixe uniquement les proportions entre les côtés. Ces proportions ont des noms, et une notation spécifique existe pour les écrire : a/c = sin A : "le sinus (ou sinus) de A" Il suffit de se rappeler : sin A se réfère au petit côté en face de l'angle A, en haut de la fraction Il y a une relation simple entre le sinus et le cosinus de n'importe quel angle . Le théorème de Pythagore indique que : a2 + b2 = c2 Par conséquent, pour tout angle A (sin A)2 + (cos A)2 = (b2/c2) + (a2/c2) = (a2 + b2)/c2 = 1 Ce rapport est habituellement écrit sin2A ( pas sinA2, qui pourrait indiquer le sinus d'un angle égal à A2): sin2A + cos2A = 1 Le sinA et le cosA sont forcément des nombres plus petits que 1, parce que les côtés adjacents et opposés d'un triangle sont toujours plus courts que celui qui est en face de l'angle droit (c'est l'hypoténuse, un mot cher aux amateurs de charades et autres rébus). Si l'angle A se rapproche de plus en plus de 90° ( B devient plus en plus petit ), le triangle devient de plus en plus étroit et fin. La longueur du côté a tend vers celle de c, alors que la longueur de b devient très petite : Plus A s'approche de 90°, plus sinA tend vers1 et cosA vers zero. Pour le calcul de quelques autres valeurs, voyez la prochaine section. |
|
A ce propos : la première table de sinus a été établie par Al-Khorezmi, qui vécut à Bagdad vers 780-850 et qui nous a également transmis le terme algèbre. Les calculatrices portatives d'aujourd'hui donnent ses résultats sur la simple poussée d'un bouton.
L'origine du nom "sinus" ( sinus en latin veut dire "compartiment") est intéressante. Comme le système décimal, elle est d'origine indienne et a été adaptée par les mathématiciens arabes à l'époque d''Al-Khorezmi. Ils ont traduit en caractères différents l'équivalent indien de sinus, sans ses voyelles (que les Arabes n'écrivent pas ) et cela a donné jb. En 1085 le Roi (espagnol) Alphonse VI de Castille repris Tolède aux arabes, dont une importante bibliothèque contenant beaucoup de manuscrits arabes, y compris des traductions de livres grecs jusque là inconnus du reste de l'Europe. Alphonse embaucha des érudits pour traduire progressivement ces livres en latin. En 1145 l'un de ces traducteurs, Robert de Chester, traduisit l' "algèbre"d' Al-Khorezmi . Dans ce livre il rencontra le mot "jb" et, ne réalisant pas qu'il s'agissait d'un mot étranger à l'arabe, se demanda quelle était sa signification dans cette langue. En ajoutant les voyelles appropriées , il trouva "compartiment", qui en latin était "sinus." Ce fut sa traduction et le terme est toujours utilisé. C'est dans sa signification correcte qu'il est employé en médecine, comme dans "sinusite" où il signifie inflammation des cavités ("sinus nasaux") s'étendant du nez vers les yeux. |
D'autres fonctions trigonométriques existent, comme la tangente de A, présentée dans la section M-12, qui s'écrit : Pour la tangente, c' est le côté opposé qui est au dessus de la barre de fraction, pour la cotangente, c'est le côté adjacent. |
Chronologie
Glossaire
Aide mathématique
Revenir
à la liste principale
Mail au Dr.Stern: stargaze("at" symbol)phy6.org
