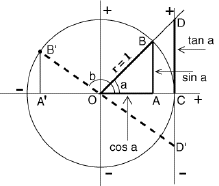
"Stargazers" décrit de deux façons le repérage de la position d'un point P sur un plan (par exemple sur une feuille du papier) : les coordonnées cartésiennes (x,y) et les coordonnées polaires (r,φ).

Toutes deux prennent comme référence un point O ("origine") et une droite tracée à partir de celui ci ("axe des abscisses"). Dans les coordonnées cartésiennes un deuxième "axe des ordonnées" est mené depuis O, perpendiculaire au premier, et des lignes parallèles à ces axes sont alors tracées depuis P, coupant les axes aux points A et B sur le schéma. Des distances OA et OB résultent alors les deux nombres qui définissent P, les coordonnées x et y de ce point.

Dans les coordonnées polaires le point P est défini par sa distance r à l'origine O (voyez le dessin) et par son angle polaire ("azimuth" sur une carte) entre l'axe des abscisses et le "rayon" r = OA, mesuré dans le sens contraire des aiguilles d'une montre.

Puisque la figure OAPB est un rectangle, la distance AP vaut aussi y. Par conséquent

sinφ = y/r
cosφ = x/r

En multipliant l'un ou l'autre par r on obtient la relation entre les deux systèmes de coordonnées ( il est entendu que des symboles voisins sont multipliés) :

x = r cosφ
y = r sinφ

Ces relations permettent de calculer (x,y) si (r,φ) sont connus. Pour calculer l'inverse -- (x,y)sont donnés, il faut trouver (r,φ)--on remarque que dans le triangle OAP, selon Pythagore :

x² + y² = r²

Par conséquent, (x,y) étant connus, on peut calculer r, et ensuite (sinφ, cosφ) , comme précédemment :

sinφ = y/r
cosφ = x/r

(Excepté au point O d'origine, où (x, y, r) valant tous zéro entraînent des fractions de type 0/0 , d'ou n'importe quelle valeur pour l'angle φ).

Cependant, il reste un problème. L' angle φ défini ci-dessus peut s'étendre de 0 à 360°, mais (sinφ, cosφ) f) ne sont définis que pour 0 à 90°, seulement pour la partie du plan où x et y sont positifs. Quand l'un ou les deux sont negatifs, l'angle φ est supérieur à 90 degrés, et ce genre d'angle n'apparaît jamais dans un triangle droit. Quel concept donner à (sinφ, cosφ) si φ est plus grand que 90 degrés ?

Il y a cependant une solution simple, en utilisant les équations qui viennent d'être vues pour redéfinir sinφ et cosφ pour ces grands angles ! Les équations sont

sinφ = y/r
cosφ = x/r

On les considère maintenant comme de nouvelles définitions du sinus et du cosinus, liées à l'angle polaire φ calculé d'après x et y (une façon légèrement différente de formuler cette définition est décrite ci-dessous). Si (x,y) sont deux positifs, le résultat est exactement le même que pour les angles intérieurs d'un triangle rectangle. Mais cela fonctionne également pour des angles plus grands. Le sinus et le cosinus peuvent maintenant être négatifs (juste comme x et y) mais leur grandeur ne peut dépasser 1, parce que la valeur de x et de y n'est jamais plus supérieure à r. Voici ces signes :

En tournant autour de son origine, la ligne OP permet à l'angle φ de se développer plusieurs fois au delà de 360°; le sinus et le cosinus restent définis comme y/r et x/r, et retrouvent leurs valeurs précédentes. De même, la rotation de OA dans la direction inverse -- dans le sens des aiguilles d'une montre - permet de définir des valeurs négatives de φ. Ensemble, ces extensions définissent (sinφ, cosφ) pour tout angle φ, positif ou négatif, de toute taille.

La relation dérivée du théorème de Pythagore

sin²φ + cos²φ = 1

reste valable pour n' importe quel de ces angles. Si un sinus ou un cosinus vaut zéro, l'autre fonction est nécessairement +1 ou -1, selon le signe de la coordonnée (x or y) qui le définit. à 90° et 270°, x = 0 donc cosφ = 0, tandis que pour 0°et 180° y = 0 et donc sinφ = 0. Nous obtenons alors :

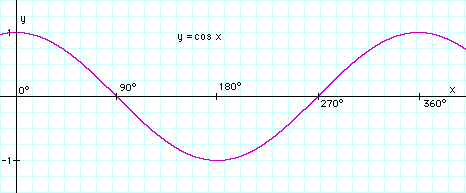
Naturellement, φ = 0° et φ = 360° représentent la même position de r par rapport à la branche positive de l'axe des abscisses. Ci-dessous la courbe évolutive de cos φ:

Une Définition légèrement différente : le Cercle - Unité

De nombreux textes de trigonométrie définissent le sinus et le cosinus un peu différemment, en utilisant ce qui est appelé " cercle - unité ". C'est un cercle dont le rayon vaut 1 unité ( quelques soient les unités choisies ). Le centre de ce cercle marque l'origine O des coordonnées (x,y), et on imagine qu'un rayon mobile OB fait un angle a avec l'axe des abscisses.

Alors la distance AB ("la ligne de sinus") égale sin a, et la distance OA ("la ligne de cosinus") égale cos a. la "ligne de tangente" est CD, tangente au cercle, et coupant la prolongation de OB, elle vaut tan a (Cela explique pourquoi le mot "tangente" correspond à cette quantité.)

Supposez que le rayon tourne jusqu'en OB', de sorte que son angle avec l'axe des abscisses devienne b, plus grand que 90°. Dans ce cas la ligne de sinus A'B' reste positive, puisqu'elle est au-dessus de l'axe horizontal. Toutefois la ligne de cosinus OA' étant à gauche de l'origine, sa longueur -- qui donne le cosinus -- doit être comptée négativement. La tangente est maintenant CD', la prolongation du rayon tournant OD', et sa longueur est aussi comptée négativement.

En laissant le rayon tourner autour du cercle et en mesurant les distances successives - en comptant négativement leurs prolongements sous l'axe horizontal et à gauche de l'axe vertical -- nous constatons que les lignes de sinus, de cosinus et de tangente donnent toujours des fonctions correctes. Elle ne sont pas vraiment différentes de la définition précédente : mais si jamais vous vous demandiez ce que le terme "tangente" avait à voir avec la trigonométrie, maintenant vous le savez ! .