Orbite geostazionarie
Tutte le orbite nello spazio obbediscono alle leggi di Keplero e di Newton. Come si è già fatto notare, per un'orbita circolare la terza legge di Keplero può essere scritta
T = 5063 secondi R3/2 = 5063 secondi R * √R
dove T è il periodo orbitale, * indica la moltiplicazione, R è il raggio dell'orbita in unità di raggi terrestri (= 6371 km) e √R è la radice quadrata di R.
 |
Il satellite per comunicazioni
TDRRS della NASA, usato
per rinviare i dati da veicoli
spaziali in orbita. |
Da questa relazione si ricava che per T = 86400 sec = 24 ore, R = 6,6 raggi terrestri. Un satellite equatoriale che i trovi quindi a questa distanza ha un periodo di 24 ore, e perciò, dato che la Terra ruota, si troverà sempre sopra lo stesso punto dell'equatore terrestre.
(Più accuratamente, il periodo orbitale dura, rispetto alle 24 ore, 235,9 secondi di meno, ed è questo il vero periodo di rotazione della Terra).
Una tale orbita è ideale per un satellite per comunicazioni, e pertanto un "paraboloide satellitare" puntato verso di esso non deve essere riposizionato per inseguirlo nel cielo, ma può rimanere puntato verso una direzione fissa.
È stato lo scrittore inglese di fantascienza Arthur Clarke che per primo propose questa "orbita geostazionaria" (o "sincrona"), molto prima che venissero lanciati i primi satelliti artificiali. Clarke scrisse in seguito "Fontane del Paradiso" (ambientato nello Sri Lanka, dove si era trasferito) in cui sottili cavi collegavano i satelliti geostazionari al suolo terrestre. Un materiale abbastanza leggero e resistente per un tale tipo di cavi non esiste, ed è così lontano da tutto ciò che è conosciuto che sarà probabilmente impossibile realizzarlo in futuro. Ma il racconto è comunque interessante. Al giorno d'oggi circa 200 satelliti geostazionari sono stati posti in orbita, alcuni di proprietà di governi per usi riservati, ma la maggior parte sono gestiti da compagnie di telecomunicazioni.
Il rientro nell'atmosfera
La formula di Keplero vale anche per un'orbita ellittica, purché si sostituisca R con il semiasse maggiore dell'orbita. Col tempo tuttavia le orbite si discostano dalle esatte ellissi kepleriane a cause di altre forze, come l'attrazione del Sole e della Luna. Per ellissi molto allungate, la conseguenza è che il punto più basso dell'orbita (il "perigeo") si sposta in su e giù, e alla fine raggiunge l'atmosfera terrestre, causando così la perdita del satellite.
Inoltre l'attrito atmosferico fa sì che satelliti ad orbita bassa prima o poi rientrino nell'atmosfera: questi satelliti, perdendo energia, scendono sempre più profondamente nell'atmosfera, e infine raggiungono gli strati più densi, dove si bruciano. Questo è stato il destino della stazione spaziale Skylab nel luglio 1979: la NASA sperava di poter usare la Navetta Spaziale per spingere il satellite su un'orbita più alta, ma la Navetta non fu pronta in tempo.
Nel frattempo era anche arrivato il picco del ciclo undecennale delle macchie solari, con una intensità maggiore di quanto sperato dalla NASA, portando una grande quantità di raggi X e di radiazioni nell'estremo ultravioletto da parte del Sole. Queste radiazioni vengono assorbite dalle frange superiori dell'atmosfera terrestre, scaldandola e facendola espandere ulteriormente verso l'esterno, soprattutto durante i "massimi solari". L'espansione dell'atmosfera aumentò la resistenza dell'aria ("l'attrito") sul moto dello Skylab, causandone la prematura fine.
Il rigonfiamento del globo terrestre
Se la Terra fosse una sfera perfetta, nei calcoli orbitali si potrebbe assumere che tutta la sua massa sia concentrata nel centro: l'effetto delle forze, almeno fuori della superficie terrestre, sarebbe esattamente lo stesso. Tuttavia la forza centrifuga associata con la rotazione della Terra la rende leggermente non sferica, con un diametro equatoriale maggiore di qualche chilometro rispetto al diametro polare.
Questo fatto influisce sull'orbita dei satelliti e bisogna tenerne conto. Quando il piano orbitale è inclinato rispetto all'equatore, il rigonfiamento equatoriale fa ruotare leggermente questo piano attorno alla Terra: una linea perpendicolare al piano orbitale descrive progressivamente un cono. È interessante notare che esiste una situazione in cui si può trarre vantaggio da questa rotazione.
In genere l'orbita di un satellite è fissa nello spazio e, mentre la Terra compie la sua rivoluzione attorno al Sole, l'orientazione di quest'orbita rispetto al Sole cambia continuamente. Prendiamo per esempio il caso di un satellite ad orbita bassa il cui piano orbitale contenga l'asse terrestre (cioè che passi esattamente sul polo nord e sul polo sud). Se in giugno quel piano è allineato con la direzione alba-crepuscolo, cioè con la linea di separazione tra la zona della Terra illuminata dal Sole e quella non illuminata, allora in settembre sarà allineato con la direzione mezzogiorno-mezzanotte, con una rotazione di 90 gradi. Si noti che allora l'orbita in giugno è sempre al Sole per tutte le 24 ore, mentre in settembre non lo è.
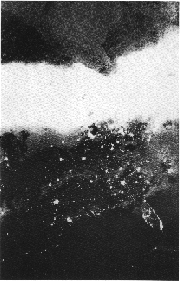
Tuttavia esistono certe orbite, che passano ad appena pochi gradi dai poli, i cui piani vengono fatti ruotare dal rigonfiamento terrestre esattamente di una rotazione all'anno. Tali orbite "sincronizzate con il Sole" possono essere progettate in modo da essere sempre al Sole, oppure mai illuminate dal Sole. I satelliti DMSP hanno orbite di questo tipo (la foto qui a lato, con l'aurora sopra i Grandi Laghi, è stata ripresa da uno di questi satelliti; si noti la Florida in basso a destra), come pure i satelliti Magsat.
Anche i satelliti per l'osservazione della Terra come il Landsat e lo SPOT ("Satellite Pour l'Observation de la Terre", Satellite Per l'Osservazione della Terra) preferiscono orbite sincronizzate con il Sole, in modo da garantire che le foto in date diverse siano sempre riprese alla stessa ora del giorno. Altrimenti la differenza nelle ombre potrebbe confondere la loro interpretazione.
I punti lagrangiani
Per la terza legge di Keplero, un veicolo spaziale che giri intorno al Sole in un'orbita circolare più piccola dell'orbita terrestre avrà un periodo di rivoluzione più breve e si muoverà più velocemente, e, se lanciato dalla Terra, la sua distanza aumenterà finché sia ben lontano dalla Terra. Esiste però un modo per tenere insieme i due oggetti.
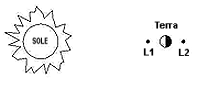
Se il veicolo spaziale è posto tra la Terra e il Sole, l'attrazione contraria della Terra riduce l'attrazione effettiva del Sole, permettendo al veicolo di muoversi in orbita attorno al Sole più lentamente. Se la distanza è scelta in modo opportuno, il moto orbitale sarà sincronizzato con quello della Terra, permettendo così ai due corpi di rimanere insieme durante la rivoluzione annuale intorno al Sole.
Il punto dove questo fenomeno avviene è il punto lagrangiano L1 (da Giuseppe Lagrange, il matematico italo-francese che per primo ne mise in luce le proprietà). Si trova a circa 4 volte la distanza della Luna e a circa 1/100 della distanza dal Sole. La prossima sezione riporta il calcolo della distanza di L1, usando i risultati delle sezioni (20), (21) e (M-5).
Il punto L1 fornisce una posizione molto utile per tenere sotto osservazione il vento solare prima che raggiunga la Terra e anche per altri scopi. Attualmente due veicoli spaziali sono posizionati vicino a L1 -- la sonda ACE, per studiare i "raggi cosmici anomali" e anche per osservare il vento solare, e la sonda SOHO, per osservare il Sole. La sonda WIND, che pure aveva occupato questa regione, è stata spostata su un'altra orbita.
La sonda SOHO, una missione congiunta tra la NASA e l'Agenzia Spaziale Europea, andò quasi perduta nel giugno 1998, quando per un incidente la sua antenna ad alto guadagno si spostò in una direzione non più puntata verso la Terra. La sonda perdette anche potenza, poiché le sue celle solari non erano più rivolte frontalmente verso il Sole, e il propellente del suo motore a razzo si era ghiacciato. Seguirono alcuni mesi di ansia, durante i quali i controllori tentarono varie manovre per riprendere il controllo, usando perfino il radiotelescopio gigante di Arecibo come un'antenna radar per individuare la posizione del veicolo. Il controllo fu recuperato nella seconda metà del settembre 1998 e il veicolo spaziale riprese la sua attività. Purtroppo il suo ultimo giroscopio andò in avaria nel dicembre 1998. Nell'aprile del 1999 si è riusciti con successo a controllare il suo assetto mediante dei volani inerziali, adattati a questo scopo anche se non erano stati progettati per questo.
Esistono altri quattro punti lagrangiani nel sistema Terra-Sole, incluso il punto L2, simmetrico a L1, dalla parte della Terra non illuminata dal Sole. Il 30 giugno 2001 la NASA ha lanciato il Microwave Anisotropy Probe (MAP) ("Sonda per l'Anisotropia delle Microonde"). Questa sonda rappresenta la continuazione del successo del Cosmic Background Explorer (COBE) ("Analizzatore del Fondo Cosmico"), che nel 1992 aveva misurato accuratamente la radiazione a microonde, residuo del "Big Bang", quando l'universo iniziò la sua esistenza (si possono leggere in proposito "Una breve storia del tempo" di Stephen Hawking, o "I primi tre minuti" di Steve Weinberg).
L'intensità della radiazione osservata dalla sonda COBE era quasi uguale in tutte le direzioni ("isotropa"), ma non completamente: rimaneva una piccola disuniformità ("anisotropia"), e la sonda MAP è stata progettata per osservarla meglio. Questa disuniformità potrebbe essere un indizio di una distribuzione irregolare della materia subito dopo il Big Bang, quando il volume dell'universo era ancora piccolo e quelle radiazioni a microonde iniziarono come raggi gamma di alta energia. La distribuzione non uniforme può essere correlata al fatto, osservato, che la materia nell'universo attuale sembra raggruppata in galassie distinte, con grandi regioni vuote tra di esse.
La NASA sta anche progettando di mettere in orbita un Telescopio Spaziale di Nuova Generazione ("Next Generation Space Telescope", NGST), il successore del telescopio orbitante Hubble, nel punto L2 o nelle sue vicinanze. Per maggiori dettagli a proposito di questi punti e delle relative missioni spaziali, si può fare clic qui.
Il punto L3 si trova dall'altra parte del Sole, invisibile dalla Terra, instabile e probabilmente poco importante. Di grande interesse sono invece i punti L4 e L5, che si trovano sull'orbita terrestre ma spostati di 60° rispetto alla linea Terra-Sole (guardando l'orbita terrestre dall'alto del polo nord, L5 si trova a 60° in verso orario rispetto a quella linea, L4 a 60° in verso antiorario). La dimostrazione matematica che un oggetto in uno di questi due punti compie un'orbita intorno al Sole con lo stesso periodo della Terra, mantenendo un angolo fisso rispetto alla linea Terra-Sole, è piuttosto lunga. Chi ha familiarità con l'algebra e la trigonometria e ha la pazienza di seguire un lungo calcolo, può trovare la dimostrazione nella sezione #34b di questo sito Web.
Se non ci fossero interferenze da parte di altri pianeti, L4 e L5 sarebbero delle posizioni stabili per eventuali piccoli terzi corpi che manterrebbero una posizione fissa rispetto alla Terra. Altri corpi vicini a tali orbite rimarrebbero vicini ad essi. Sembra che siano stati osservati dei piccoli asteroidi vicino ai punti L4 e L5 della Terra, di Marte e di Venere, ma l'effetto è molto più pronunciato per i punti lagrangiani di Giove, il più grande di tutti i pianeti. Centinaia di cosiddetti Asteroidi Troiani sono stati localizzati nelle vicinanze dei punti L4 e L5 di Giove, i quali descrivono un'orbita attorno al Sole con lo stesso periodo di Giove. Questi asteroidi sono chiamati "Troiani", poiché i loro nomi sono quelli dei personaggi dell'Iliade di Omero.
Anche il sistema Terra-Luna ha i suoi punti lagrangiani, e i punti L4 e L5 sull'orbita lunare sono stati proposti come posizioni per "colonie spaziali" autosufficienti.
|



