(34a) The Distance to the L1 Point

Index

30.To Space by Cannon?

30a.Project HARP

31.Nuclear Spaceflight?

32. Solar Sails

32a. Early Warning of
Solar Shocks

33. Ion Rockets

34.Orbits in Space

34a. L1 Lagrangian pt.

34b. L4/L5 Points (1)

34c.L4/L5 Points (2)

35. Gravity Assist

36. Pelton Turbine

Afterword

By using the tools of sections (20) and (21), the mathematics of approximate solutions developed in (M-5), and assuming all orbits are circles, it is a relatively straightforward job to calculate the distance to the Lagrangian L1 point (or to L2). We start by repeating the derivation of Kepler's 3rd law for circular orbits.

Note:

Let the gravitational constant be denoted by G, the mass of the Sun by M, that of Earth by m, the Earth's distance from the Sun by r and its velocity in its orbit by v. By applying what was learned about gravity and about centripetal and centrifugal forces, we then get (as in section (20))

GMm/r² = mv²/r
and multiplying both sides by r/m

GM/r = v²

If T is the orbital period, since the distance covered by the Earth each orbit is 2πr,

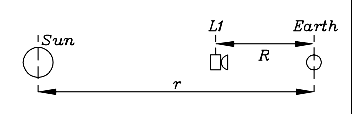
vT = 2π r Divide by T v = 2π r/T Square: v² = 4π²r²/T² and therefore GM/ r = 4π²r²/T² Divide both sides by r²: GM/ r³ = 4π²/T²
from which Kepler's 3rd law for circular orbits follows.

Consider next a spacecraft of mass m_sc , located on the line connecting the Earth and the Sun, between those two at a distance R from Earth and (r–R) from the Sun (drawing). The force F pulling it sunward is decreased by the pull of the Earth in the opposite direction, so

F = GMm_sc/(r–R)² – Gmm_sc/R²

Assume that this spacecraft also moves in a circle around the Sun, with velocity v_sc. Then if the centrifugal force balances the attraction (or else, the attraction supplies the centripetal force)

GMm_sc/(r–R)² – Gmm_sc/R² = m_scv_sc²/(r–R)

In a similar way to the earlier calculation, both sides are multiplied by (r–R)/m_sc, giving

GM/(r–R) – Gm(r–R)/R² = (v_sc)²

We assume that the spacecraft also moves in a circle around the Sun, of radius (r–R). (That of course requires the Earth to be always in place to pull in the opposite direction from the Sun, a subject to which we will return shortly). The orbital period T_sc of the satellite then satisfies, as before

v_scT_sc = 2π(r–R) from which (v_sc)² = 4π²(r–R)²/(T_sc)² We then have

GM/(r–R) – Gm(r–R)/R² = 4π²(r–R)²/(T_sc)²

or, dividing everything by (r–R)²

GM/(r–R)³ – Gm/R²(r–R) = 4π²/(T_sc)²

which resembles the earlier "3rd law" equation, except that the Earth's opposing pull is now added. But will the Earth be always located where its pull on the satellite is exactly opposite to the Sun? No, unless the two orbital periods are the same

T_sc = T

Only then does the spacecraft's motion match that of the Earth and the distance between the two stays constant. That in general only happens at one value of R, that is, only at one distance from the Earth, and that distance R is now the unknown number we need to derive, the "thing" that we seek. Witgh T_sc = T, one may substitute Kepler's 3rd law for Earth alone, derived earlier:

GM/ r³ = 4π²/T²s Substituting

GM/(r–R)³ – Gm/R²(r–R) = GM/r³

Let us divide both sides by GM: then G disappears from the scene, and in place of the masses (m,M) of (Earth,Sun) we only have their ratio, a small number y, about

y = m/M = 3/1,000,000

or in scientific notation (the dot meaning multiplication)

y = m/M = 3/10⁶ (or 3.10^-6)

The equation is now

1/(r–R)³ – y/R²(r–R) = 1/r³

Multiply both sides by r³

r³/(r–R)³ – y r³/R²(r–R) = 1

In each of the fractions, divide both top and bottom by r³ . Since any fraction having the same top and bottom equals 1, that is the same as multiplying by 1, and does not change anything]. Also, rename R/r to become a new variable z. Then

1/(1-z)³ – y/z²(1-z) = 1

Now we are ready to roll, to derive the unknown quantity z. The above equation is complicated--in fact, a simple formula for its solution probably does not exist. However, since z is small, it is rather easy to get an approximate solution, using the methods of section (M-5). There is was shown that when z is very small ,

1/(1-z)³ ~ 1 + 3z and [y/z²]/(1-z) ~ [y/z²] (1+z)

Substituting these approximations in the main equation gives

1 + 3z – [y/z²] (1+z) ~ 1 From this 3z ~ [y/z²] (1+z) and hence 3z³ ~ y(1+z)

Both sides are now equally small. The right-hand side is only slightly modified by the addition of z: we may drop this term without making much difference. Then

3z³ ~ y = 3/1,000,000

z³ ~ 1/1,000,000 Take 3rd root of both sides R/r = z ~ 1/100 = 0.01

Thus the distance to L1 is about 0.01 of the distance to the Sun. It is now possible to go back to more exact equations, like 3z³ ~ y(1+z), and replace z on the right by its approximate value 0.01, to get more accurate solutions. Such a process of gradual improvement, called iteration, is also used with Kepler's equation, discussed in section (12a). Because of the smallness of z, these modifications turn out here to make very little difference.

The derivation of the distance to the nightside Lagrangian point L2 is very similar (as is its result). In that case the equations involve r+R rather than r–R, and in the equation for F the terms are added instead of subtracted, because now the Sun and the Earth pull in the same direction. Try it!

Questions from Users: Stability of Lagrangian points
*** Is L2 in the Earth's Shadow?

Optional: #34b The L4 and L5 Lagrangian Points

Next Stop: #35 To the Planets, to the Stars

Timeline Glossary Back to the Master List

Author and Curator: Dr. David P. Stern
Mail to Dr.Stern: stargaze("at" symbol)phy6.org .

Updated: 12.13.2001 ; Re-formatted 27 March 2006 ; Edited 26 October 2016

Disclaimer: The following material is being kept online for archival purposes.

Although accurate at the time of publication, it is no longer being updated. The page may contain broken links or outdated information, and parts may not function in current web browsers.

(34a) The Distance to the L1 Point

Above is background material for archival reference only.