Weightlessness

    An astronaut in low Earth orbit moves in (approximately) a big circle extending around the Earth. The acceleration required for such motion is provided by gravity

mg(R_E/r)²= mv²/r

    where the astronaut's weight mg on the Earth's surface at r = R_E is adjusted on the left side for the greater distance. That is of course the same equation as the one used to demonstrate Newton's study of gravity. However, it can also be written

mg (r/R_E)² – mv²/r = 0

    That can be interpreted as stating that in the astronaut's frame of reference, all bodies are subject to two forces, gravity and the centrifugal force, and the two are in perfect balance, adding up to zero.

    It is sometimes claimed that astronauts in space are in a "zero gravity" environment, but actually they are still very much under the influence of the Earth's gravity. True, the astronaut observes no tendency at all to fall towards Earth, but the reason is different and can be stated in one of two ways:

1. Gravity is already kept fully occupied by supplying the ongoing acceleration (the first of the above equations); or

2. The force of gravity is perfectly balanced by the centrifugal force (second equation).

Weightlessness Simulation in an Airplane

Then the equation of motion of an object subject to F alone is

    The acceleration a is what a spacecraft in orbit experiences, viewed from the fixed frame of the Earth. In a circular orbit of radius r it equals v²/r, while in an elliptic orbit it may have a different magnitude and different direction, which could also be calculated. The important thing to note here is that an astronaut inside that spacecraft is subject to the same gravity and therefore undergoes the same acceleration as the spacecraft itself. Viewing the astronaut's motion in the frame of the moving spacecraft, the astronaut is not pulled towards the floor of the cabin or in any other direction, and therefore has the impression that gravity has been eliminated.

    Suppose that instead, the astronaut rode inside a freely falling cabin, near the surface of the Earth. There, too

but since r is very close to 1 R_E, we may set that ratio equal to 1 and get simply

    The cabin falls with acceleration g, but the passenger also falls with the same acceleration, so again, no force exists that pushes the passenger towards the floor of the cabin. Acting on cues from the surrounding cabin, the passenger will again get the illusion that gravity did not exist.

It makes no difference if the cabin started with a constant velocity--e.g. tossed upwards with an initial velocity u and with an initial horizontal velocity w--because neither of these affects the forces and accelerations. Both cabin and passenger would still be accelerating downwards at a=g, creating an illusion of zero gravity.

    If this experiment were actually conducted, that illusion and also the cabin would all too soon be shattered by contact with the hard ground below. Furthermore, air resistance would soon reduce the cabin's acceleration below g. The passenger inside, still subject to a=g, would then overtake the cabin, a process which would appear in the frame of the cabin like a partial return of gravity.

    However, the same experiment can be safely performed aboard a high-flying aircraft, which could match any air resistance by the thrust of its engines. By following a programmed parabolic path similar to that of a projectile subject to gravity alone, such an aircraft can create--for a limited time--a zero-gravity environment inside its cabin.

    NASA has done so with a KC-135 aircraft (reported to be now retired), a 4-engine jet nicknamed "The Vomit Comet" because its sudden transition to zero-g made some passengers quite airsick. The airplane could produce a temporary zero-g environment in its cabin, and was used for training astronauts and for short experiments on zero-gravity phenomena. The cargo space inside it was completely covered with padding, and a "zero gravity" illusion could be maintained for about 20-30 seconds.

The Coriolis Force

Wheel-shaped space  station with visiting   winged spaceship (Von Braun's, from the early 1950's)

    The science-fiction film "2001: A Space Odyssey" featured spinning space station, whose rotation provided the crew with "artificial gravity." It was a wheel-shaped structure, with hollow spokes connecting the wheel to a cabin in the center (drawing). The cabin in the middle was where transfers between the station and visiting spacecraft took place. Click here for more on that design.

    Given such a rotation, something like gravity would indeed be produced, with "down" being towards the outside (Larry Niven expanded that notion into the fanciful science-fiction novel "Ringworld" and its sequels). When calculating this effect it is simplest to use the station's frame of reference and add a centrifugal force to all other forces there.

    However, when one moves in this rotating environment, especially motion up and down the spokes, an additional force is encountered, named for the Frenchman Gaspard Gustave de Coriolis (1792-1843).

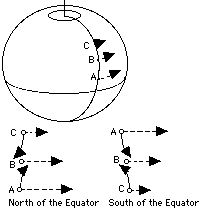
    Imagine an astronaut moving along one of the spokes, say from point A in the drawing to point B--most likely, climbing a ladder, since such motion goes against the station's "artificial gravity." At any point, as viewed in the frame of the outside world, the astronaut is also rotating around the station's axis.

    At both point A and B, the rotation is in the same direction, but at B it is slower, because that point is nearer to the axis of rotation and therefore describes a smaller circle. What happens at B to the extra speed the astronaut had at A? According to Newton's first law, loosely applied, the astronaut would tend to keep that extra speed and would therefore be pushed agains the side of the spoke (direction of the arrows). That push is the Coriolis force. When the motion is in the opposite direction, from B to A, the direction of the force is. . . the same or reversed? Work it out yourself!

Swirling Water in a Bathroom Sink

From time to time the claim is made that water draining from bathroom sinks swirls in opposite directions north and south of the equator.

    The physical principle is sound, but the actual effect is so microscopic that it is unlikely to be observed in the draining of bathroom sinks. On the other hand, the same effect is very important in large-scale swirling of the atmosphere, in hurricanes and typhoons as well as in ordinary weather patterns.

    The Earth, when viewed from above the north pole, spins counter-clockwise. Imagine 3 points in the northern hemisphere, at the same geographical longitude (drawing)--A is closest to the equator, B is somewhat poleward and C further poleward still. Each of these points covers in one day a full circle around the Earth's axis: A has the biggest circle, goes the greatest distance and therefore moves the fastest, B with a small circle moves more slowly, and C is even slower. The points are redrawn at the bottom on a magnified scale, with dashed arrows indicating the directions and magnitude of the velocity of the surface of the Earth at each point.

    Next consider the air above those points. If no wind is blowing, the air moves together with the surface. Its velocity viewed from the outside ("Frame of the Universe") is given by the dashed arrows, but its velocity relative to the surface of the Earth is everywhere zero. In the frame of the rotating Earth it stays at the points (A,B,C) and does not leave them.

    Suppose now that for some meteorological reason, a low atmospheric pressure develops at B. Air from A and C will flow towards it, heading (in the frame of the Earth) north and south, respectively. Newton's laws, however, apply without modification only in the outside frame, and there every mass of air tends to keep its eastward velocity. The air from C will therefore lag behind the ground below it, whose eastward motion is faster. The air from A, on the other hand, will move faster and overtake the ground. As a result, the flows of air relative to the Earth (solid arrows) are not simply southward and northward, but will bend as shown, creating a counterclockwise swirl around B.

    By similar arguments you can convince yourself that south of the equator the swirl is clockwise. Note that these arguments are based on viewing the motion from the outside. If we wish to solve the motion strictly in the frame of the rotating Earth (as atmospheric scientists do), it turns out that we need add two additional terms to Newton's equations. One is the centrifugal force, acting on all objects. The other is the Coriolis force, acting only on moving objects (or fluids) and responsible for the swirling effect described here.    

A hurricane viewed from space.

Next Stop: Your Choice!

#25 The Principle of the Rocket continues to the story of spaceflight.

The Sun: Introduction opens a group of sections studying our Sun, from many different angles (spaceflight comes later).

            Timeline                     Glossary                     Back to the Master List

Author and Curator:   Dr. David P. Stern
     Mail to Dr.Stern:   stargaze("at" symbol)phy6.org .