Work is associated with forces that overcome resistance. The work W performed while overcoming a resisting force F over a distance x is defined as F times x

    Things to note: F must oppose the motion. If the direction of the vector F differs from the direction of x, then F must be resolved into components parallel and perpendicular to x (in the manner discussed in section 14) and only the parallel component directly opposing the motion is used in the formula for W.
    And if F varies in the course of the motion, an appropriate average value must be used in the formula for W. (You will need calculus to derive that average.)

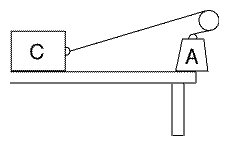
    Suppose we lift a weight A of mass m a distance h (for height) from the floor to the table (Figure 1). The force we must overcome is

    That, however, is just the potential energy added to the weight! We could tie the weight by a string to a similar weight on the floor--denoted B --and pass the string over a pulley. Then--with an ideal pulley having no friction, and an ideal string having no weight--if the mass on the table is pushed over the edge, the slightest downward push will make it descend all the way to the floor, while B is raised to the level of the table.

    Work W was performed in raising mass B, while mass A has given up its potential energy. That shows energy is indeed "ability to perform work": potential energy was given up, and in return work was performed.

    The work performed in raising B was again invested in potential energy. With ideal pulleys, strings etc., that energy again equals W, illustrating the conservation of energy. In an ideal set-up with no losses, this energy could be used to raise A to its previous height. Note that our working definition "energy is anything that can turn a machine" also holds, since a dropping weight could indeed turn a machine.

    Energy is always preserved but--as seen in an earlier section--not always in a usable form. Suppose the weight A is tied, not to an equal weight on the floor, but to a block of concrete on a table (Figure 2). If the force of sliding friction of the block on the tabletop is exactly equal to mg, then dropping A allows the block to slide a distance h and overcome F along it.

    But now the potential energy mgh has been converted to heat, generated by friction. This is energy too--but energy dispersed on the molecular level, hard to convert back to work. And as noted in section 15 on energy, even with ideal devices and substances, physics can at most promise the recovery of a certain fraction of that energy, never all of it.

Tidbit:
  The two weights A and B in the first drawing illustrate the principle of the funicular railways, short railways with a straight track leading steeply up a hill or mountain. Funicular railways always have two short trains (sometimes, of a single carriage each), connected by a steel cable. The cable goes from one train to the mountain top, where it wraps a few times around a drum turned by a motor, and then it continues down again, to the other train.

  Because the trains are linked, when one goes up, the other descends, and by giving up its potential energy, it helps pull the other one upwards. Any in-between stations must always be coordinated, so that when the ascending train stops at station X, the descending train stops at station Y (and later, with the ascending train at Y, the descending one is at X). When one train is reaches the bottom station, the other reaches the top station.

  One would think that two tracks are needed, one for each train. Actually, one track is enough, if halfway up where the trains meet, a short double section is inserted, with switches that automatically route the trains to a separate tracks, allowing them to pass safely. Gondolas suspended from cables and taking tourists to the tops of scenic mountains may also be connected in pairs like this, but they always hang from separate cables.