(M-11a) Exercices de Trigonométrie
|
Les sections (M-6)-(M-11) vous ont donné quelques principes de trigonométrie. Cette section vous permettra de les appliquer en pratique. Dans certains cas les solutions sont données, mais n'allez pas les voir avant d'avoir fait l'effort personnel de les résoudre.
|
|
Nous avons essayé d'éviter les répétition des mêmes exercices : chaque ensemble est différent. Faites-les tous -- n'en omettez pas ! On suppose que vous avez une calculatrice pour calculer les sinus et cosinus, avec également les fonctions sin-1 et cos-1 qui permettent une fois sinA ou cosA connu de trouver l'angle A, dans la gamme 0 à 180 degrés.
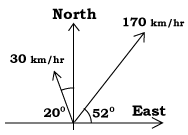
 (La solution suit : ne la consultez qu'après avoir solutionné le problème vous-même. Les enseignants peuvent substituer différents nombres et directions) Notons V le vecteur de vitesse de l'avion relativement à l'air, W celle du vent relativement à la terre, et U=V+W, la vitesse de l'avion relativement à la terre, où l'addition est l'un des vecteurs. Tracez un diagramme avec les vitesses et les angles donnés convenablement reproduits. Pour effectuer l'addition réelle chaque vecteur doit être résolu en ses composants. Nous obtenons
Ajoutez :
Par conséquent
|
|
|
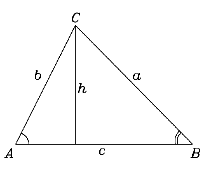
Le problème : Sur le triangle ABC, la ligne AB représente la rive d'une rivière rectiligne. Nous mesurons la distance c = AB =118 mètres, et les angles A et B sont de 63° et 55°. Quelle est la distance b = AC ? Ne lisez pas la solution avant d'avoir essayé de la trouver. En classe, les professeurs dans la classe peuvent substituer différents nombres et directions.
|
|
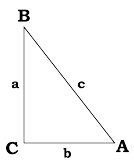
Puisque la somme des angles est de 180 degrés, l'angle C doit être égal à 62°. Donc, de par la loi des sinus : Multipliez les deux côtés par sin(55) pour obtenir la longueur b = CA Nouvelle question : quelle est la distance perpendiculaire de C à la ligne c = AB ? (conseil : elle égale la hauteur h comme dans le problème (4).)
|
|
|
Si cette formule n'est pas applicable de façon ou d'autre, le faisceau ne peut pas quitter le verre mais est réfléchi à nouveau dans le verre depuis la surface - frontière, comme si c'était un miroir ("réflexion interne totale") Le problème : B est donné = 0, 20, 90, 60, 80 -- que deviennent les angles A ? Y a-t-il des faisceaux qui ne traversent pas le verre ?
|
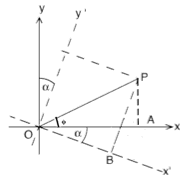
Rappelez-vous : dans un triangle rectangle avec un angle α , si vous multipliez le grand côté
Réécrivons le résultat final :
Exercice d'algèbre : : en utilisant les deux relations ci-dessus, pouvez-vous exprimer (x,y) en termes de (x', y ') ? Il faut employer sin2α + cos2α = 1.
Cela doit être également conforme à la figure, puisqu'alors (x,y) sont obtenus en tournant (x', y ') d'un angle α , dans le sens contraire des aiguilles d'une montre, ce qui peut être considéré comme la rotation dans le sens des aiguilles d'une montre d' un angle (–α ).
|
Revenir à la liste principale
Mail au Dr.Stern: stargaze("at" symbol)phy6.org