(18c) Il lavoro
|
Il concetto di lavoro è connesso strettamente con quello di energia. In effetti, la definizione formale di energia è "la capacità di compiere un lavoro". Vediamo che cosa significa tutto questo.
Il lavoro è associato a una forza che vince una resistenza. Il lavoro W effettuato contro una forza resistente F su una distanza x è definito come F moltiplicato x
Occorre notare: F si deve opporre al moto. Se la direzione del vettore F è diversa dalla direzione di x, allora F deve essere decomposta nelle due componenti parallela e perpendicolare a x (come è stato discusso nella sezione 14) e soltanto la componente che si oppone direttamente al moto va usata nella formula per W.
Supponiamo di sollevare un peso A di massa m su una distanza h (in altezza) dal pavimento al tavolo (Figura 1). La forza che dobbiamo vincere è
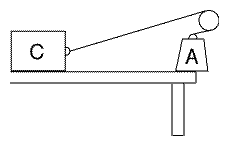
Questa, tuttavia, non è altro che l'energia potenziale che si aggiunge al peso! Possiamo collegare il peso con una corda a un altro peso -- che indicheremo con B -- che stia sul pavimento, e far passare la corda su una puleggia. Allora (considerando una puleggia ideale senza attriti e una corda ideale senza peso), se la massa che sta sul tavolo viene spinta oltre il bordo, una minima spintarella verso il basso la farà scendere fino al pavimento, mentre B salirà al livello del tavolo. È stato compiuto il lavoro W per sollevare la massa B, mentre la massa A ha ceduto la sua energia potenziale. Questo esempio mostra che l'energia è in effetti "la capacità di compiere un lavoro": viene ceduta l'energia potenziale e in cambio viene compiuto un lavoro. Il lavoro compiuto per sollevare B è stato di nuovo investito per accumulare energia potenziale. Con pulegge e corde ideali, tale energia di nuovo uguaglia W, illustrando così il principio della conservazione dell'energia. In un sistema ideale senza perdite, questa energia può essere impiegata per sollevare A fino alla sua precedente altezza. Si noti che la nostra definizione operativa "l'energia è qualsiasi cosa che possa far girare una macchina" vale ancora, poiché far scendere un peso può in effetti far girare una macchina. L'energia si conserva sempre, ma -- come si è visto in una precedente sezione -- non sempre in una forma riutilizzabile. Supponiamo che il peso A sia legato, non a un peso uguale sul pavimento, ma a un blocco di cemento sul tavolo Figura 2). Se la forza di attrito radente del blocco sulla superficie del tavolo è esattamente uguale a mg, allora, facendo cadere A, il blocco scorrerà per una distanza h vincendo la forza F lungo quel percorso. Ma in questo caso l'energia potenziale mgh è stata convertita in calore, generato dall'attrito. Anche questa è energia, ma è un'energia dispersa a livello molecolare, difficile da riconvertire in lavoro. Come si è notato nella sezione 15 sull'energia, anche con dispositivi e sostanze ideali, la fisica ci può al massimo permettere di recuperare una certa frazione di quell'energia, ma mai tutta. |
|
Curiosità: Dal momento che i due convogli sono collegati tra loro, quando uno sale l'altro scende, e, cedendo la sua energia potenziale, aiuta a tirare in su l'altro convoglio. Le varie stazioni lungo il percorso devono essere sempre coordinate, in modo che quando un convoglio in salita si ferma alla stazione X, quello in discesa si fermi alla stazione Y (e successivamente, con il convoglio in salita alla stazione Y, quello in discesa deve stare alla stazione X). Quando un convoglio raggiunge la stazione più in basso, l'altro raggiunge la stazione in cima. Si potrebbe pensare che siano necessari due binari, uno per ciascun treno. In effetti, è sufficiente un solo binario, purché a metà altezza, quando i due treni si incrociano, sia inserita una breve sezione a due binari, con degli scambi che automaticamente indirizzino ciascun treno su un binario diverso, così che si possano incrociare in tutta sicurezza. Anche i vagoncini appesi a un cavo delle funivie turistiche, che raggiungono le vette montane, sono in genere collegati a coppie allo stesso modo, ma sono appesi a cavi separati. |
Sezione facoltativa: #18d: Il lavoro contro una forza elettrica: il generatore di Van de Graaff
Il prossimo argomento: (19) Il moto circolare
Cronologia Glossario Torna alla pagina iniziale
Autore e Curatore: Dr. David P. Stern
Ci si può rivolgere al Dr. Stern per posta elettronica (in inglese,
per favore!):
stargaze("chiocciola")phy6.org
Traduzione in lingua italiana di Giuliano Pinto
Aggiornato al 14 Agosto 2005