The Law

    The ellipse traced by a planet around the Sun has a symmetric shape, but the motion is not symmetric.

    Think of a stone thrown upwards. As it rises it loses speed... then for an instant, at the top of the trajectory, it moves very slowly... and finally it comes down, gathering speed again. In many ways, a planet around the Sun, or of a scientific satellite around Earth, moves like that, too, although the equations are different.

    That is most evident if the orbit is elongated, that is, if its eccentricity is large. As the planet or satellite rises in its orbit, it slows down, then as it returns, it speeds up again. It moves fastest during closest approach, at a point of the orbit called perihelion for a planet ("helios" is the Sun) and perigee for an Earth satellite ("gee" from "geo", denoting Earth).

    After studying actual observations, mainly of Mars, Kepler proposed the following prescription for predicting the speeding-up and the slowing-down. Let a line ("radius vector") be drawn from the center of the Sun to the planet (or from the center of Earth to the satellite). Kepler's law states:

"The radius vector sweeps equal areas in equal times"

Illustrating Kepler's 2nd law:  segments AB and CD take  equal times to cover.

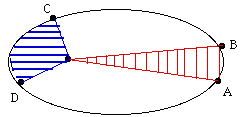
    As an example, let the drawing on the right represent the orbit of an Earth satellite, and let AB and CD be the portions of the orbit covered in 3 hours near apogee and near perigee, respectively. If then O is the Earth's center, the shaded areas OAB and OCD are equal. What it means, obviously, is that CD is much longer than AB, because near perigee the satellite moves much faster and it covers a much greater distance in 3 hours.

            Energy

[The section that follows is optional and addresses mainly motions of satellites around Earth. Motions of planets in the gravity field of the Sun, or of satellites near some other planet, follow similar laws.]

    Energy may be loosely defined as anything that can make a machine move. Our machines are usually powered by the energy of electricity or heat; light is another form of energy, converted into electricity by the solar cells which power most artificial satellites.

    Gravity can also provide energy. The wheels of grandfather clocks are turned by weights which gradually descend to the bottom of the clock, at which point they must be cranked up again, or else the clock stops. Thomas Jefferson, at his home near Charlottesville, Virginia, had a clock whose weights (hanging on the side of a room) were cannonballs strung on a rope, and to give the clock a 7-day range, a hole was cut in the floor allowing the balls to descend to the basement.

    When a weight (or cannonball) is raised against the force of gravity, it gains potential energy--energy by virtue of its position, proportional to the height to which it was raised. If the weight is dropped, it loses height and potential energy, but gains speed and kinetic energy, energy due to the speed of motion. Kinetic energy can be converted back to potential energy, as happens to a roller coaster after it passes the bottom of a dip and climbs up again.

    A similar change occurs when a stone is thrown upwards with some velocity v. If its mass is m    (mass will be defined in a later section; for now let it be a property of the stone proportional to its weight),  its kinetic energy can be shown to be

1/2 mv²

As the stone rises, v and the kinetic energy decrease, while the potential energy grows. It is given by

 h m g

where h is the height in meters and g is a constant measuring the strength of the force of gravity: if m is in kilograms, h in meters and v in meters-per-second (written m/sec; walking speed is about 1 m/sec), g is about 9.81.

The sum of the two is the total energy E₁ and by a fundamental law of mechanics it stays constant:

E₁   =   1/2 mv² +  h m g   =  constant             (1)

    As the stone rises, the kinetic part of its energy gets smaller and smaller, becoming zero when it reaches its highest point, where for a brief instant v = 0. On the downward trip, the opposite changes take place. (A later section of "Stargazers" comes back to this formula and makes it more meaningful.)

            The Mean Anomaly

(Optional)    Earlier it was stated that a third orbital element is needed to mark where the satellite is located in its orbit. Since the equation of the orbital ellipse is

r = a(1 – e²)/(1 + e cos φ)

each value of the angle φ   (φ in handwriting), called the "true anomaly," specifies a position along the orbit. One could in principle use the true anomaly as a third orbital element.

    Unfortunately, the speed of the satellite varies unevenly around its orbit, it grows larger near perigee and drops again near apogee. Kepler's 2nd law describes that variation and should lead to a formula giving φ for any time t, except that no neat formula exists for areas like those shown in blue and red in the top image.

    The simplest way of expressing the ups and downs of φ is to use two auxiliary angles, which like φ increase by 360 degrees each orbit, the "eccentric anomaly" E (the letter here has nothing to do with energy) and the mean anomaly M , with a formula [not given here] that connects φ and  E, and another that connects E and M. The way M is defined assures that it grows at a constant rate as time t advances:

M = M(0) + nt                       (5)

where M(0) is the value of M when t = 0 and n is a constant (related to the constant appearing in Kepler's third law). The mean anomaly is regarded as the third orbital element.